题目内容
已知,⊙O1与⊙O2外切,⊙O1的半径R=2,设⊙O2的半径为r,(1)如果⊙O1与⊙O2的圆心距d=4,求r的值;
(2)如果⊙O1与⊙O2的公切线中有两条互相垂直,并且r≤R,求r的值.
分析:(1)根据两圆外切,圆心距等于两圆半径之和进行计算;
(2)根据切线长定理和切线的性质定理发现两个等腰直角三角形,根据等腰直角三角形的性质得到方程进行计算.
(2)根据切线长定理和切线的性质定理发现两个等腰直角三角形,根据等腰直角三角形的性质得到方程进行计算.
解答:解:(1)如图,根据相外切两圆的性质得出:r=4-2=2;
(2)如图:根据切线长定理得到等腰直角三角形,
则有2+r=
(2-r):
则r=6-4
;
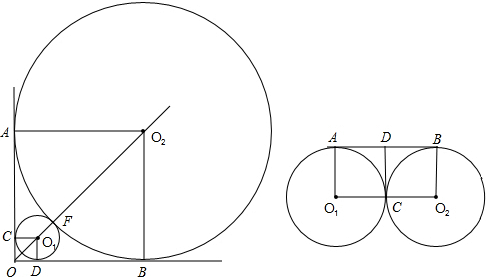
当是第二情况时,当R=r时,如图,此时四边形AO1O2B、AO1CD、DCO2B都是矩形,
即此时R=r=2;
即r=6-4
或2.
(2)如图:根据切线长定理得到等腰直角三角形,
则有2+r=
| 2 |
则r=6-4
| 2 |
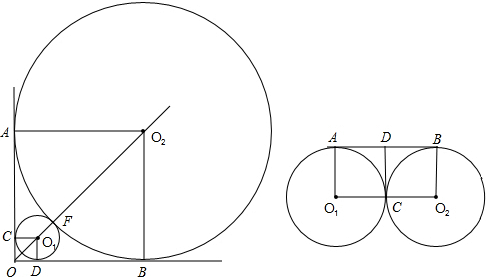
当是第二情况时,当R=r时,如图,此时四边形AO1O2B、AO1CD、DCO2B都是矩形,
即此时R=r=2;
即r=6-4
| 2 |
点评:考查了两圆的位置关系与数量之间的联系,能够熟练运用切线的性质定理和切线长定理.根据等腰直角三角形的性质找到线段之间的关系.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.
11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.