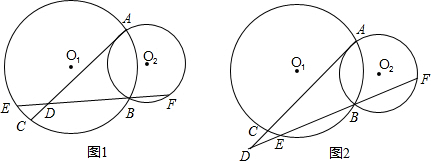
题目内容
已知:⊙O1与⊙O2相交于A、B两点,⊙O1的切线AC交⊙O2于点C.直线EF过点B交⊙O1于点E,交⊙O2于点F.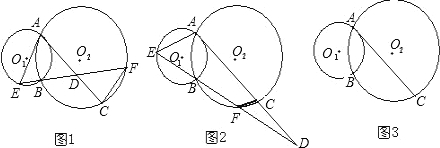
(1)若直线EF交弦AC于点K时(如图1).求证:AE∥CF;
(2)若直线EF交弦AC的延长线于点时(如图2).求证:DA•DF=DC•DE;
(3)若直线EF交弦AC的反向延长线于点(在图3自作),试判断(1)、(2)中的结论是否成立并证明你的正确判断.
分析:(1)连接AB.根据弦切角定理和圆周角定理的推论,可以证明∠E=∠1=∠F,即可证明结论;
(2)根据弦切角定理、圆内接四边形的性质,证明平行线,再根据相似三角形的判定和性质求解;
(3)正确画出图形后,显然只需构造弦切角所夹的弧所对的圆周角,再结合圆周角定理的推论,即可证明平行,再根据相似三角形的判定和性质,即可证明.
(2)根据弦切角定理、圆内接四边形的性质,证明平行线,再根据相似三角形的判定和性质求解;
(3)正确画出图形后,显然只需构造弦切角所夹的弧所对的圆周角,再结合圆周角定理的推论,即可证明平行,再根据相似三角形的判定和性质,即可证明.
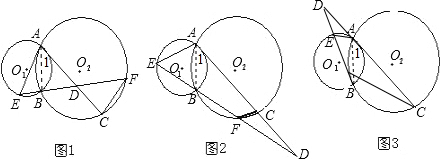
解答:(1)证明:连接AB.
∵AC是⊙O1的切线,
∴∠E=∠1,
又∵∠F=∠1.
∴∠E=∠F.
∴AE∥CF.
(2)证明:连接AB.
∵AC是⊙O1的切线,
∴∠E=∠1,
又∵A、B、F、C在⊙O2上,
∴∠2=∠1.
∴∠E=∠2,
又∠D=∠D,
∴△ADE∽△CDF.
∴
=
,
∴DA•DF=DC•DE.
(3)解:(1)(2)中的结论都成立.
证明:如图3.
∵∠C=∠B=∠DAE,
∴AE∥CF.
又∠D=∠D,
∴△ADE∽△CDF.
∴
=
,
∴DA•DF=DC•DE.

∵AC是⊙O1的切线,
∴∠E=∠1,
又∵∠F=∠1.
∴∠E=∠F.
∴AE∥CF.
(2)证明:连接AB.
∵AC是⊙O1的切线,
∴∠E=∠1,
又∵A、B、F、C在⊙O2上,
∴∠2=∠1.
∴∠E=∠2,
又∠D=∠D,
∴△ADE∽△CDF.
∴
| DA |
| DC |
| DE |
| DF |
∴DA•DF=DC•DE.
(3)解:(1)(2)中的结论都成立.
证明:如图3.
∵∠C=∠B=∠DAE,
∴AE∥CF.
又∠D=∠D,
∴△ADE∽△CDF.
∴
| DA |
| DC |
| DE |
| DF |
∴DA•DF=DC•DE.
点评:连接相交弦是相交两圆中常见的辅助线.综合运用了弦切角定理、圆周角定理的推论、圆内接四边形的性质以及相似三角形的性质和判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.
11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.