题目内容
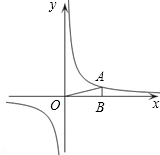
在反比例函数y= (x>0)的图象上,有一系列点A1、A2、A3、…、An、An+1,若A1的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A1、A2、A3、…、An、An+1作x轴与y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1= ,S1+S2+S3+…+Sn= .(用n的代数式表示).
(x>0)的图象上,有一系列点A1、A2、A3、…、An、An+1,若A1的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A1、A2、A3、…、An、An+1作x轴与y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1= ,S1+S2+S3+…+Sn= .(用n的代数式表示).
5 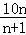
解析试题分析:由已知条件横坐标成等差数列,再根据点A1、A2、A3、…、An、An+1在反比例函数上,求出各点坐标,再由面积公式求出Sn的表达式,把n=1代入求得S1的值.
解:∵点A1、A2、A3、…、An、An+1在反比例函数y= (x>0)的图象上,且每点的横坐标与它前一个点的横坐标的差都为2,
(x>0)的图象上,且每点的横坐标与它前一个点的横坐标的差都为2,
又点A1的横坐标为2,
∴A1(2,5),A2(4,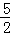 )
)
∴S1=2×(5﹣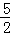 )=5;
)=5;
由题图象知,An(2n,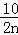 ),An+1(2n+2,
),An+1(2n+2,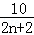 ),
),
∴S2=2×(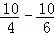 )=
)=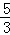 ,
,
∴图中阴影部分的面积知:Sn=2×(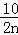
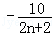 )=
)=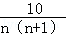 ,(n=1,2,3,…)
,(n=1,2,3,…)
∵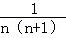 =
=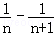 ,
,
∴S1+S2+S3+…+Sn=10( +
+ +…+
+…+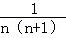 )=10(1
)=10(1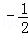
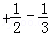
 )=
)=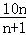 .
.
故答案为: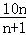 .
.
考点:反比例函数综合题.
点评:此题是一道规律题,首先根据反比例函数的性质及图象,求出An的坐标的表达式,再由此求出Sn的表达式.

练习册系列答案
相关题目
点(1,2)在反比例函数y=
的图象上,则k的值是( )
| 1-k |
| x |
| A、0 | B、1 | C、-1 | D、-2 |
 如图,在直角坐标系中,O为坐标原点.已知反比例函数y=
如图,在直角坐标系中,O为坐标原点.已知反比例函数y=