题目内容
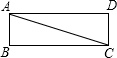
在矩形ABCD中,AB=a,AD=2b(a>2b>0),E是AD的中点,BF⊥EC,垂足为F,求BF的长(用含有a、b的代数式表示).


在Rt△CDE中,根据勾股定理有:
CE=
=
.
∵AD∥BC,
∴∠CED=∠BCF.
∵∠D=∠BFC=90°,
∴△CED∽△BCF,
∴
=
,
∴BF=
=
=
.
CE=
| CD2+DE2 |
| a2+b2 |
∵AD∥BC,
∴∠CED=∠BCF.
∵∠D=∠BFC=90°,
∴△CED∽△BCF,
∴
| BF |
| CD |
| BC |
| CE |
∴BF=
| BC×CD |
| CE |
| 2b×a | ||
|
2ab
| ||
| a2+b2 |

练习册系列答案
相关题目