题目内容
如图：矩形ABCD的对角线AC=8cm，∠CAD=15°，则矩形ABCD的面积S=______cm2．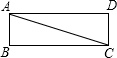
如图：取∠DCE=60°，CE交AD于E，
∵四边形ABCD是矩形，
∴∠D=∠BCD=90°，
∵∠CAD=15°，
∴∠ACD=75°，
∴∠ACE=∠ACD-∠DCE=75°-60°=15°，
∴∠ACE=∠CAD，
∴AE=CE，∠DEC=∠EAC+∠ECA=30°，
在Rt△DCE中，EC=2DC，
DE=
=
=
DC，
设DC=xcm，则DE=
xcm，AE=EC=2xcm，
∴AD=AE+DE=（2+
）xcm，
在Rt△ACD中，AD2+CD2=AC2，
∵AC=8cm，
∴[（2+
）x]2+x2=64，
解得：x2=32-16
，
∴矩形ABCD的面积S=AD•CD=（2+
）x2=（2+
）（32-16
）=16（cm2）．
故答案为：16．
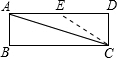
∵四边形ABCD是矩形，
∴∠D=∠BCD=90°，
∵∠CAD=15°，
∴∠ACD=75°，
∴∠ACE=∠ACD-∠DCE=75°-60°=15°，
∴∠ACE=∠CAD，
∴AE=CE，∠DEC=∠EAC+∠ECA=30°，
在Rt△DCE中，EC=2DC，
DE=
| DC |
| tan∠DEC |
| DC |
| tan30° |
| 3 |
设DC=xcm，则DE=
| 3 |
∴AD=AE+DE=（2+
| 3 |
在Rt△ACD中，AD2+CD2=AC2，
∵AC=8cm，
∴[（2+
| 3 |
解得：x2=32-16
| 3 |
∴矩形ABCD的面积S=AD•CD=（2+
| 3 |
| 3 |
| 3 |
故答案为：16．
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
．