题目内容
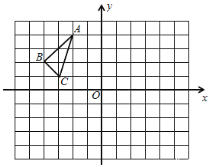
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3),以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O、B、C的对应点分别为D、E、F,且点D恰好落在BC边上.
(1)在原图上画出旋转后的矩形;
(2)求此时点D的坐标.

【答案】(1)见解析(2)(1,3)
【解析】
(1)根据题意作出图形即可;
(2)根据矩形的性质得到AC=OB=3,OA=BC=5,∠OBC=∠C=90°,根据旋转的性质得到AD=AO=5,由勾股定理即可得到结论.
(1)如图所示,矩形AFED即为所求,
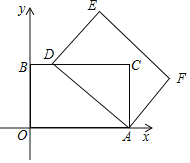
(2)∵A(5,0),B(0,3),
∴OA=5,OB=3,
∵四边形AOBC是矩形,
∴AC=OB=3,OA=BC=5,∠OBC=∠C=90°,
∵矩形ADEF是由矩形AOBC旋转得到,
∴AD=AO=5,
在Rt△ADC中,CD=![]() =4,
=4,
∴BD=BC-CD=1,
∴D(1,3).

练习册系列答案
相关题目