题目内容
【题目】（1）计算：|﹣
|+（﹣1）2019+2sin30°+（
）0
（2）解方程：
【答案】（1）
；（2）x=-3
【解析】
（1）利用绝对值代数意义、有理数的乘方、特殊角的三角函数值、零指数幂计算出各个数值，再运用实数的混合运算法则计算即可；
（2）直接利用分式方程的解法解方程即可．
解：（1）|﹣
|+（﹣1）2019+2sin30°+（
﹣
）0
＝+（﹣1）+2×+1
＝+（﹣1）+1+1
＝
（2）方程两边同乘以（x－2）得：x2＋2＋x－2＝6，
则x2＋x－6＝0，
（x－2）（x＋3）＝0，
解得：x1＝2，x2＝﹣3，
检验：当x＝2时，x－2＝0，故x＝2不是方程的根，
当x＝﹣3时，x－2＝﹣3－2＝﹣5≠0
故x＝﹣3是分式方程的解．
练习册系列答案
阅读快车系列答案
相关题目
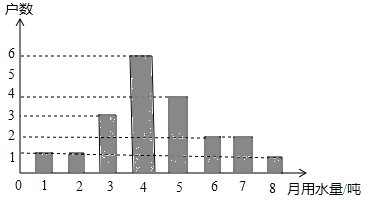
【题目】九（1）班同学为了解某小区家庭月均用水情况（单位：吨），随机调查了该小区部分家庭，并将调查数据进行如下整理：
月均用水量 | 频数（户） | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
25 | 2 | 0.04 |
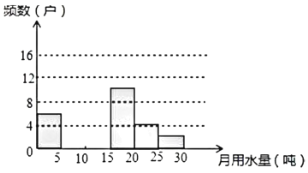
请解答以下问题：
（1）把上面的频数分布表和频数分布直方图补充完整；
（2）若该小区有1000户家庭，根据调查数据估计，该小区月均有水量超过20吨的家庭大约有多少户？
【题目】我市华润生活超市准备一次性购进A、B两种品牌的饮料100箱，此两种饮料每箱的进价和售价如下表所示
设购进A种饮料x箱，且所购进的两种饮料能全部卖出，获得的总利润为y元．
品牌 | A | B |
进价 | 65 | 49 |
售价 | 80 | 62 |
求y关于x的函数关系式；
由于资金周转原因，用于超市购进A、B两种饮料的总费用不超过5600元，并要求获得利润不低于1380元，则从两种饮料箱数上考虑，共有哪几种进货方案？
利润
售价
进价
