题目内容
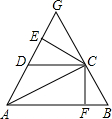
如图，梯形ABCD中，AB∥DC，AD=DC=CB，AD、BC的延长线相交于G，CE⊥AG于E，CF⊥AB于F，则图中共有全等三角形（ ）
| A．1对 | B．2对 | C．3对 | D．4对 |
∵AB∥DC，AD=DC=CB，
∴梯形ABCD是等腰梯形，
∴∠B=∠DAB=∠EDC，
在Rt△EDC和Rt△FBC中，
∵
，
∴△ECD≌△FBC（ASA）
∵AD=DC，
∴∠DAC=∠DCA，
又∵∠DCA=∠CAB，
∴∠DAC=∠CAB，
∴AC是∠GAB的角平分线，
∴CE=CF，
在Rt△ACE和Rt△ACF中，
∵
∴△ACE≌△ACF（HL）．
综上可得有两对全等三角形．
故选：B．
∴梯形ABCD是等腰梯形，
∴∠B=∠DAB=∠EDC，
在Rt△EDC和Rt△FBC中，
∵
|
∴△ECD≌△FBC（ASA）
∵AD=DC，
∴∠DAC=∠DCA，
又∵∠DCA=∠CAB，
∴∠DAC=∠CAB，
∴AC是∠GAB的角平分线，
∴CE=CF，
在Rt△ACE和Rt△ACF中，
∵
|
∴△ACE≌△ACF（HL）．
综上可得有两对全等三角形．
故选：B．
练习册系列答案
天天练口算系列答案
相关题目
