��Ŀ����
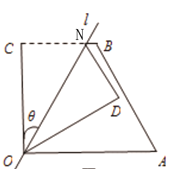
����Ŀ����ͼ1���ı���OABC�У�OA=a��OC=5��BC=3,��AOC=��BCO=90�㣬������O��ֱ��l���ı��ηֳ������֣�ֱ��l��OC���ɵĽ���Ϊ�ȣ����ı���OABC��ֱ�ǡ�OCB��ֱ��l�۵�����C���ڵ�D������ͼ1����
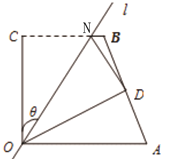
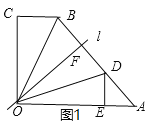
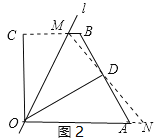
ͼ1 ͼ2 ͼ3
��1������=45�㣬�ı���OABC��ֱ�ǡ�OCB��ֱ��l�۵���B���ڵ��ı���OABC�ı�AB�� (��ͼ2) ����a��ֵ. ![]()
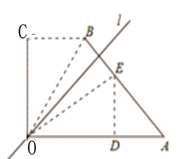
��2�����۵����DǡΪAB���е㣨��ͼ3������ȵ�ֵ��
���𰸡���1��8����2��30��.
�������������������1����ͼ1�����÷��۱任�����ʵõ�OE=OC=5��DE=BC=3��֤��AE=DE�����⼴�ɽ����
��2����ͼ2���������ߣ�����֤��DM=DN������֤����AOD=��DOM=��MOC=�������⼴�ɽ����
�����������1����ͼ1��������ã�
l��AB��OE=OC=5��DE=BC=3��
��OED=��C=90�㣻
�ߡ�AOF=45�㣬l��AB��
���A=45�㣬��ADE=90��-45��=45�㣬
���A=��ADE��
��AE=DE=3��
��OA=5+3=8��
��a��ֵΪ8��
��2����ͼ2������MD���ӳ�����OA���ӳ����ڵ�N��
��BM��AN��
���BMD�ס�AND��
��![]() ����BD=AD��
����BD=AD��
��MD=ND��
������ã���ODM=��C=90�㣬��MOD=��MOC=�ȣ�
��OD���߶�MN�Ĵ�ֱƽ���ߣ�
��OM=ON��
��ODƽ�֡�MON��
���AOD=��DOM=��MOC=�ȣ�
�ߡ�AOC=90�㣬
����=30�㣮