题目内容
【题目】在△ABC中,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,
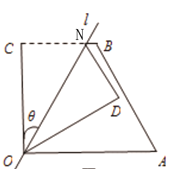
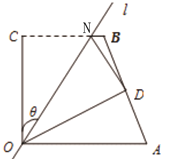
(1) 如图(1),连接AM、AN,求∠MAN的度数。
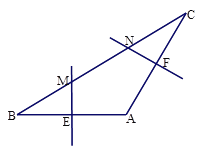
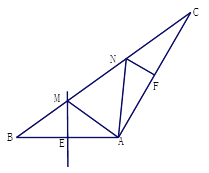
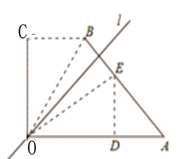
(2) 如图(2),如果AB=AC, 求证:BM=MN=NC.
【答案】(1)60 (2)见解析
【解析】试题分析:(1)由AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,根据线段垂直平分线的性质,可得AM=BM,AN=CN,继而求得∠B=∠BAM=30°,∠C=∠CAN=30°,则可求得∠MAN的大小;
(2)由∠B=∠BAM=30°,∠C=∠CAN=30°,易证得△AMN是等边三角形,则可证得BM=MN=NC.
试题解析:
(1)∠MAN=60°.
理由:∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵ME是AB的垂直平分线,NF是AC的垂直平分线,
∴AM=BM,AN=CN,
∴∠B=∠BAM=30°,∠C=∠CAN=30°,
∴∠MAN=∠BAC-∠BAM-∠CAN=60°;
(2)证明:∵∠B=∠BAM=30°,∠C=∠CAN=30°,
∴∠AMN=∠ANM=60°,
∵∠MAN=60°,
∴△AMN是等边三角形,
∴AM=AN=MN,
∵AM=BM,AN=CN,
∴BM=MN=NC.

练习册系列答案
相关题目