题目内容
某学生参加社会实践活动,在景点P处测得景点B位于南偏东 方向,然后沿北偏东
方向,然后沿北偏东 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
 方向,然后沿北偏东
方向,然后沿北偏东 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
(50+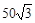 )米
)米
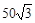 )米
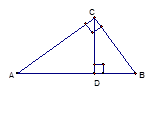
)米试题分析:过P作PD⊥AB,垂足为D,则可得AB=AD+BD,∠A=60。,∠APD=30。,且PA=100米,根据含30°角的直角三角形的性质可得AD=50米,再由∠B=∠DPB=45。,可得DB=DP,然后根据勾股定理求得DP的长,即可求得结果.
过P作PD⊥AB,垂足为D,则AB=AD+BD,
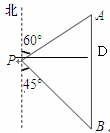
∴∠A=60。,∠APD=30。,且PA=100米,
∴AD=50米,
又∵∠B=∠DPB=45。,
∴DB=DP,
∵
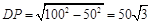
∴AB=50+
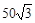 米,
米,∴景点A与景点B之间的距离为(50+
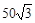 )米。
)米。点评:解题的关键是读懂题意,正确作出辅助线,构造直角三角形解题.

练习册系列答案
相关题目
 ≈1.7)
≈1.7)
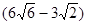 m,则电线杆AB的长度_____ m.
m,则电线杆AB的长度_____ m.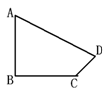

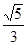
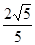


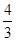
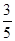
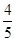
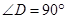 ,
,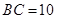 ,
,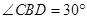 ,
,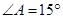 .
. 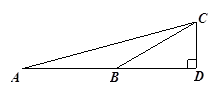
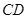 的长;
的长;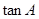 的值.
的值.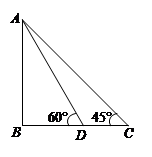
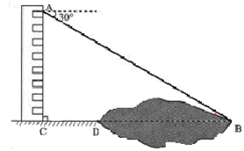
 处测得荷塘的一端
处测得荷塘的一端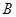 处的俯角为
处的俯角为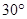 ,荷塘另一端
,荷塘另一端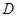 处
处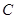 、
、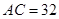 米,
米,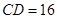 米,求荷塘宽
米,求荷塘宽 为多少米?(结果保留根号)
为多少米?(结果保留根号)