Question

【题目】如图，在△ABC和△BCD中，∠BAC=∠BCD=90°，AB=AC，CB=CD．延长CA至点E，使AE=AC；延长CB至点F，使BF=BC．连接AD，AF，DF，EF．延长DB交EF于点N．

（1）求证：AD=AF；

（2）试判断四边形ABNE的形状，并说明理由．

Answer 1

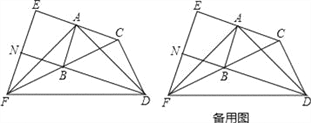
【答案】（1）证明见解析；（2）四边形ABNE是正方形，理由见解析

【解析】解：（1）证明：∵AB=AC，∠BAC=90°，

∴∠ABC=∠ACB=45°，

∴∠ABF=135°，

∵∠BCD=90°，

∴∠ABF=∠ACD，

∵CB=CD，CB=BF，∴BF=CD，

在△ABF和△ACD中，

∴△ABF≌△ACD（SAS），

∴AD=AF；

（2）答：四边形ABNE是正方形；理由如下：

证明：由（1）知，AF=AD，△ABF≌△ACD，

∴∠FAB=∠DAC，

∵∠BAC=90°，

∴∠EAB=∠BAC=90°，

∴∠EAF=∠BAD，

在△AEF和△ABD中，

∴△AEF≌△ABD（SAS），

∴BD=EF；

∵CD=CB，∠BCD=90°，

∴∠CBD=45°，

∵∠EAB=90°，△AEF≌△ABD，

∴∠AEF=∠ABD=90°，

∴四边形ABNE是矩形，

又∵AE=AB，

∴四边形ABNE是正方形．