题目内容
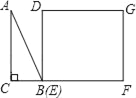
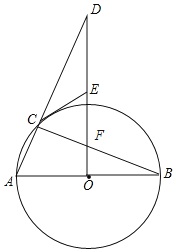
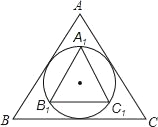
【题目】如图，若等边△A1B1C1内接于等边△ABC的内切圆，则
的值为_____．
【答案】
【解析】
由于△ABC、△A1B1C1都是等边三角形，因此它们的外心与内心重合；可过内切圆的圆心O分别作AB、A1B1的垂线，连接OA、OA1；在构建的含特殊角的直角三角形中，用⊙O的半径分别表示出AB、A1B1的长，进而可求出它们的比值．
∵△A1B1C1和△ABC都是等边三角形，
∴它们的内心与外心重合.
如图,过点O作AB的垂线,交A1B1于E,连接OA、OA1.
设圆O的半径为R.
Rt△OAD中,∵∠OAD=30°，OD=R，
∴AD=
R,即AB=2R.
Rt△OA1E中,∵∠OA1E=30°,OA1=R，
∴A1E=
R,即A1B1=R.
∴
.
练习册系列答案
相关题目
【题目】某大酒店共有豪华间 50 间，实行旅游淡季、旺季两种价格标准：
淡季 | 旺季 | |
豪华间价格（元/天） | 600 | 800 |
（1）该酒店去年淡季，开始时，平均每天入住房间数为 20 间，后来，实行降价优惠提高豪华间入住率，每降低 20 元，每天入住房间数增加 1 间．如果豪华间的某日总收入为 12500 元，则该天的豪华间实际每间价格为多少元（同天的房间价格相同）；
（2）该酒店豪华间的间数不变．经市场调查预测，如果今年旺季豪华间实行旺季价格，那么每天都客满；如果价格继续上涨，那么每增加 25 元，每天未入住房间数增加 1 间．不考虑其他因素，该酒店将豪华间的价格上涨多少元时， 豪华间的日总收入最高？最高日总收入是多少元？
