题目内容
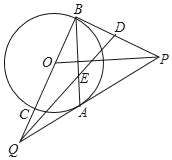
【题目】如图,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O上一点,且PA=PB,延长BO分别与⊙O、切线PA相交于C、Q两点.
(1)求证:PB是⊙O的切线;
(2)QD为PB边上的中线,若AQ=4,CQ=2,求QD的值.
【答案】(1)详见解析;(2)QD的值是![]() .
.
【解析】
(1)要证明PB是⊙O的切线,只要证明∠PBO=90°即可,根据题意可以证明△OBP≌△OAP,从而可以解答本题;
(2)根据题意和勾股定理的知识,可以求得QD的值.
(1)证明:连接OA,
在△OBP和△OAP中,
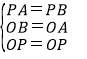 ,
,
∴△OBP≌△OAP(SSS),
∴∠OBP=∠OAP,
∵PA是⊙O的切线,A是切点,
∴∠OAP=90°,
∴∠OBP=90°,
∵OB是半径,
∴PB是⊙O的切线;
(2)连接OC
∵AQ=4,CQ=2,∠OAQ=90°,
设OA=r,
则r2+42=(r+2)2,
解得,r=3,
则OA=3,BC=6,
设BP=x,则 AP=x,
∵PB是圆O的切线,
∴∠PBQ=90°,
∴x2+(6+2)2=(x+4)2,
解得,x=6,
∴BP=6,
∴BD=3,
∴QD=![]() =
=![]() ,
,
即QD的值是![]() .
.

练习册系列答案
相关题目