Question

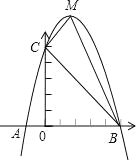
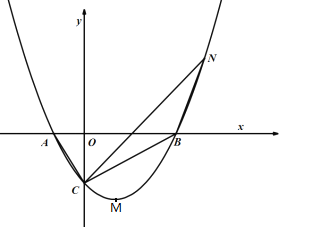
【题目】如图，抛物线，经过点.

（1）求抛物线的解析式及顶点M的坐标；

（2）连接AC、BC，N为抛物线上的点且在第一象限，当时，求N点的坐标；

（3）我们通常用表示整数的最大公约数，例如. 若，则称a、b互素，关于最大公约数有几个简单的性质：①，其中k为任意整数；②； 若点满足：a，b均为正整数，且，则称Q点为“互素正整点”，当时，该抛物线上有多少个“互素正整点”？

Answer 1

【答案】（1）抛物线的顶点M坐标为；（2）N（4，5）；（3）在时，该抛物线上有65个“互素正整点”

【解析】

（1）将A、B、C三点坐标代入中即可得到答案；

（2）设，求得直线NC的解析式为y=（t-2）x-3，设设直线CN与x轴交于点D，求出点D的坐标，根据即可列式计算得出点N的坐标；

（3）抛物线上的任意正整点R(横纵坐标为正整数的点)可以表示为，得到，找到符合条件的值即可得到答案.

（1）∵抛物线经过点A（﹣1，0），B（3，0），C（0，-3），

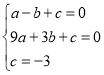解得：，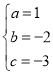

∴=,

抛物线的顶点M坐标为；

（2）∵N是抛物线上第一象限的点，

∴设（t＞0），又点C（0，-3），

设直线NC的解析式为，N在直线NC上，

解得k=t-2

∴直线NC的解析式为y=（t-2）x-3，

设直线CN与x轴交于点D，

当y=0时，x=，

∴D（，0），BD=3﹣，

∵S△NBC=S△ABC，

∴S△CDB+S△BDN=ABOC，即BD|yC﹣yN|= [3﹣（﹣1）]×3，

即×（3﹣）[3﹣（﹣t2+2t+3）]=6，

整理，得：t2﹣3t﹣4=0，

解得：t1=4，t2=﹣1（舍去），

当t=4时，t2-2t-3=5，

∴N（4，5）；

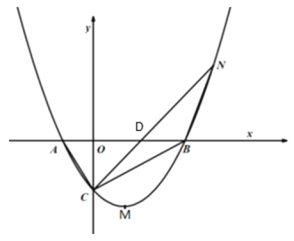
(3)抛物线上的任意正整点R(横纵坐标为正整数的点)可以表示为：

，t为正整数，且，

由性质①②，t与的最大公约数，

，

即只需满足即可，又因为3是素数，当且仅当t不是3的倍数时，t与3互素，

在4到100共97个数中，总共有32个数是3的倍数，

故共有65个数不是3的倍数，满足，

即在时，该抛物线上有65个“互素正整点”.