题目内容
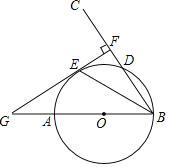
【题目】已知AB是⊙O的直径，弦CD与AB相交于点E，连接AD，BC，已知AE＝AD，∠BAD＝34°．
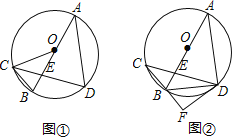
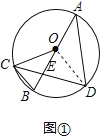
（1）如图①，连接CO，求∠ADC和∠OCD的大小；
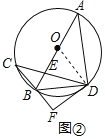
（2）如图②，过点D作⊙O的切线与CB的延长线交于点F，连接BD，求∠BDF的大小．
【答案】（1）∠ADC=73°，∠OCD=39°；（2）34°
【解析】
（1）连接OD，根据等腰三角形的性质即可得到结论；
（2）连接OD，根据切线的性质得到∠ODF=90°，根据圆周角定理得到∠ADB=90°，根据等腰三角形的性质即可得到结论．
（1）连接OD．
∵AE=AD，∠BAD=34°，∴∠ADC=∠AED
（180°﹣34°）=73°．
∵OA=OD=OC，∴∠ADO=∠A=34°，∴∠OCD=∠ODC=∠ADC﹣∠ADO=73°﹣34°=39°；
（2）连接OD．
∵DF是⊙O的切线，∴∠ODF=90°．
∵AB是⊙O的直径，∴∠ADB=90°，∴∠ADO=∠BDF．
∵OA=OD，∴∠A=∠ADO，∴∠BDF=∠BAD=34°．
练习册系列答案
相关题目
