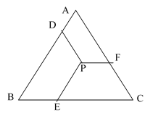
题目内容
【题目】如图，二次函数y=ax2+bx+c(a≠0)图象的一部分，对称轴为直线x=
，且经过点(2，0).下列说法：①abc<0；②a+b=0；③4a+2b+c<0；④若(-2，y1)，(
，y2)是抛物线上的两点，则y1＜y2，其中说法正确的是( )
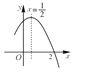
A. ①②④ B. ③④ C. ①③④ D. ①②
【答案】A
【解析】解：①∵二次函数的图象开口向下，∴a＜0，∵二次函数的图象交y轴的正半轴于一点，∴c＞0，∵对称轴是直线x=
，∴
=
，∴b=﹣a＞0，∴abc＜0．
故①正确；
②∵由①中知b=﹣a，∴a+b=0，故②正确；
③把x=2代入y=ax2+bx+c得：y=4a+2b+c，∵抛物线经过点（2，0），∴当x=2时，y=0，即4a+2b+c=0．
故③错误；
④∵（﹣2，y1）关于直线x=
的对称点的坐标是（3，y1），又∵当x＞
时，y随x的增大而减小， 
＜3，∴y1＜y2．
故④正确；
综上所述，正确的结论是①②④．
故选A．
阅读快车系列答案【题目】在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球实验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
摸到白球的频率 | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
（1）请估计：当n很大时，摸到白球的概率约为 ．（精确到0.1）
（2）估算盒子里有白球 个．
（3）若向盒子里再放入x个除颜色以外其它完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在50%，那么可以推测出x最有可能是 ．
【题目】中华文明，源远流长；中华汉字，寓意深广，为传承中华优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写大赛”
为了解本次大赛的成绩，校团委随机抽取了其中若干名学生的成绩作为样本进行统计，制成如下不完整的统计图表：
成绩 | 频数 | 频率 |
| 10 |
|
| 30 |
|
| 40 | n |
| m |
|
| 50 |
|
a | 1 |
请根据所给信息，解答下列问题：
______，
______，
______；
补全频数直方图；
这若干名学生成绩的中位数会落在______分数段；
若成绩在90分以上
包括90分
的为“优”等，请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人？
