题目内容
已知关于![]() 的方程
的方程![]() .
.
(1)求证:无论![]() 取任何实数时,方程恒有实数根;
取任何实数时,方程恒有实数根;
(2)若![]() 为整数,且抛物线
为整数,且抛物线![]() 与
与![]() 轴两交点间的距离为2,求抛物线的解析式;
轴两交点间的距离为2,求抛物线的解析式;
(3)若直线![]() 与(2) 中的抛物线没有交点,求
与(2) 中的抛物线没有交点,求![]() 的取值范围.
的取值范围.
解:(1)分两种情况讨论.
① 当![]() 时,方程为
时,方程为![]()
![]()
∴![]() 方程有实数根 -----------------------------1分
方程有实数根 -----------------------------1分
②当![]() ,则一元二次方程的根的判别式
,则一元二次方程的根的判别式
![]()
=![]()
∴不论![]() 为何实数,
为何实数,![]() 成立,
成立,
∴方程恒有实数根 -----------------------------------------3分
综合①、②,可知![]() 取任何实数,方程
取任何实数,方程![]() 恒有实数根
恒有实数根
(2)设![]() 为抛物线
为抛物线![]() 与
与![]() 轴交点的横坐标.
轴交点的横坐标.
令![]() , 则
, 则 ![]()
由求根公式得,![]() ,
,![]() -------------------------------------4分
-------------------------------------4分
∴抛物线![]() 不论
不论![]() 为任何不为0
为任何不为0
的实数时恒过定点![]()
∵ ![]()
∴ ![]()
∴ ![]() 或
或![]() ,--------------------------------------------5分
,--------------------------------------------5分
∴ ![]() 或
或![]() (舍去)
(舍去)
∴求抛物线解析式为![]() , -------------------------6分
, -------------------------6分
(3)由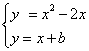 ,得
,得![]()
∴![]()
∵直线![]() 与抛物线
与抛物线![]() 没有交点
没有交点
∴![]()
∴![]()
所以,当![]() ,
,
直线![]() 与(2)中的抛物线没有交点.
与(2)中的抛物线没有交点.
------------------------------------------------------------8分

练习册系列答案
相关题目
已知关于的方程
=-1有正根,则实数a的取值范围是( )
| x+a |
| x-3 |
| A、a<0且a≠-3 |
| B、a>0 |
| C、a<-3 |
| D、a<3且a≠-3 |
 的方程
的方程 .
.
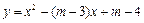 与
与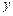 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求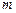 的值.
的值.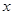 的方程
的方程
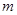 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)