Question

【题目】已知A、B是数轴上的两个点，点A表示的数为13，点B表示的数为－5，动点P从点B出发，以每秒4个单位长度的速度沿数轴向右匀速运动，设运动时间为秒．

（1）BP= ，点P表示的数 （分别用含的代数式表示）；

（2）点P运动多少秒时，PB=2PA？

（3）若M为BP的中点，N为PA的中点，点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长．

Answer 1

【答案】（1），；（2）3秒或9秒；（3）长度不发生变化，长度是9．

【解析】试题分析：(1)根据BP=速度×时间可表示出BP的长，点P表示的数为-5+4t；

(2) 分点P在AB之间运动时和点P在运动到点A的右侧时两种情况列出方程求解即可;

(3) 分点P在AB之间运动时和点P在运动到点A的右侧时两种情况,利用中点的定义和线段的和差求出MN的长即可.

解：（1）由题意得，BP=4t，点P表示的数是-5+4t；

（2）当点P在AB之间运动时，由题意得，

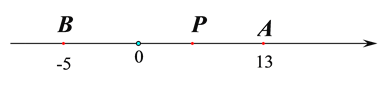
PB=4t，PA=13-（-5+4t）=18-4 t，

∵PB=2PA，

∴4t=2（18-4 t），

∴t=3;

当点P在运动到点A的右侧时，由题意得，

PB=4t，PA=-5+4t-13=4 t -18，

∵PB=2PA，

∴4t=2（4 t -18），

∴t=9;

综上可知，点P运动多3秒或9秒时，PB=2PA.

（3）当点P在AB之间运动时，由题意得，

PB=4t，PA=18-4 t，

∵M为BP的中点，N为PA的中点，

∴，,

∴MN=MP+NP=2t+9-2t=9;

当点P在运动到点A的右侧时，由题意得，

PB=4t，PA=4 t -18，

∵M为BP的中点，N为PA的中点，

∴，,

∴MN=MP-NP=2t-（2t-9）=9;

综上可知，线段MN的长度不发生变化，长度是9.