Question

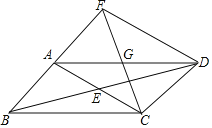
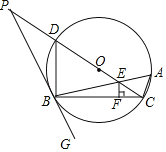
【题目】如图，在Rt△ABC中，AC=BC，∠ACB=90°，点D、E分别在AC、BC上，BD与AE交于点O，且CD=CE，若点F是BD的中点，连接CF，交AE于点G．

（1）求证：CF⊥AE；

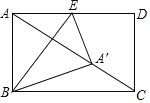
（2）如图2，过点F作FM⊥BC，交AE的延长线于点M，垂足为M，连接CF，若CG=GM．

①求证：CF=CM；

②求的值．

Answer 1

【答案】（1）详见解析；（2）①详见解析；②

【解析】

证明≌，结合直角三角形斜边中线的性质解决问题即可．

证明四边形CDFM是平行四边形，即可解决问题．

连接EF，设，证明，把问题转化为：，求出OG，用a表示，即可解决问题．

（1）证明：如图1中，

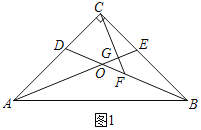
∵AC=BC，∠ACE=∠BCD=90°，CE=CD，

∴△ACE≌△BCD（SAS），

∴∠CAE=∠CBD，

∵DF=FB，

∴CF=FD=FB，

∴∠FCB=∠FBC，

∴∠FCB=∠CAB，

∵∠CAB+∠AEC=90°，

∴∠AEC+∠FCB=90°，

∴∠CGE=90°，

∴CF⊥AE．

（2）①证明：如图2中，

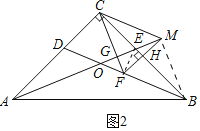
∵FM⊥BC，

∴∠FHC=∠CGE=∠MGF=90°，

∴∠ECG+∠CEG=90°，∠ECG+∠CFH=90°，

∴∠CEG=∠CFH，

∴CG=GM，

∴△CGE≌△MGF（AAS），

∴CE=FM，EG=GF，

∵CD=CE，

∴CD=FM，

∵∠FHB=∠ACB=90°，

∴CD∥FM，

∴四边形CDFM是平行四边形，

∴CM=DF，

∵CF=DF=FB，

∴CM=CF．

②连接EF，BM．设FG=EG=a，

∵CM=BF，CM∥BF，

∴FG∥BM，

∴=，

∵△CAE≌△CBD，

∴∠CAE=∠CBD，∵∠CAB=∠CBA，

∴∠OAB=∠OBA，

∴OA=OB，

∴=，

易知OG=GF=EG=a，EF=EM=a，

∴OM=2a+a，

∴==．