题目内容
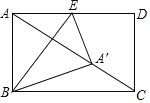
【题目】如图,矩形ABCD中,点E为AD的中点,连结BE,将△ABE沿BE翻折,点A恰好落在AC上的点A处,若AB=2,则AC的长度为_____.
【答案】2![]()
【解析】
连接A'D,设BE与AC交于点M,由翻折知,BE垂直平分AA',证明△ABM≌△CDA',推出A'C=AM,再证明△BAM∽△CAB,设AM=A'M=A'C=x,则AC=3x,通过相似三角形对应边的比相等可求出x的值,进一步求出AC的长度.
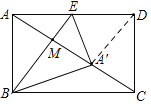
解:如图,连接A'D,设BE与AC交于点M,
由翻折知,BE垂直平分AA',
∴AB=A'B=2,AM=A'M,AE=A'E,
∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,∠ABC=90°,
∴∠DCA=∠BAC,
∵点E为AD的中点,
∴AE=DE=A'E,
∴点A,A',D三点在以AD为直径的圆上,
∴∠DA'A=∠DA'C=90°=∠AMB,
∴△ABM≌△CDA'(AAS),
∴A'C=AM,
∴AM=A'M=A'C,
∵∠ABC=∠ANB=90°,∠BAM=∠BAM,
∴△BAM∽△CAB,
∴![]() ,
,
设AM=A'M=A'C=x,则AC=3x,
∴![]() ,
,
解得,x=![]() (取正值),
(取正值),
∴3x=2![]() ,
,
∴AC=2![]() ,
,
故答案为:2![]() .
.

练习册系列答案
相关题目