题目内容
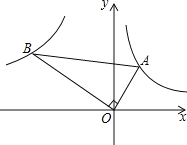
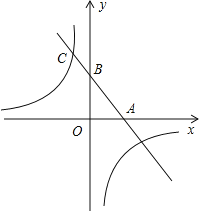
【题目】如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③![]() ;④(a﹣b)2S△EFO=b2S△DGO.其中结论正确的个数是( )
;④(a﹣b)2S△EFO=b2S△DGO.其中结论正确的个数是( )

A. 4个B. 3个C. 2个D. 1个
【答案】B
【解析】
试题由四边形ABCD和四边形CEFG是正方形,根据正方形的性质,即可得BC=DC,CG=CE,∠BCD=∠ECG=90°,则可根据SAS证得①△BCG≌△DCE;然后延长BG交DE于点H,根据全等三角形的对应角相等,求得∠CDE+∠DGH=90°,则可得②BH⊥DE.由△DGF与△DCE相似即可判定③错误,由△GOD与△FOE相似即可求得④.
试题解析:①∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
在△BCG和△DCE中,
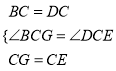 ,
,
∴△BCG≌△DCE(SAS),
故①正确;
②延长BG交DE于点H,
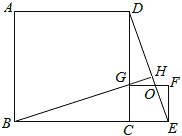
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
又∵∠CBG+∠BGC=90°,
∴∠CDE+∠DGH=90°,
∴∠DHG=90°,
∴BH⊥DE;
∴BG⊥DE.
故②正确;
③∵四边形GCEF是正方形,
∴GF∥CE,
∴![]() ,
,
∴![]() 是错误的.
是错误的.
故③错误;
④∵DC∥EF,
∴∠GDO=∠OEF,
∵∠GOD=∠FOE,
∴△OGD∽△OFE,
∴![]() ,
,
∴(a-b)2S△EFO=b2S△DGO.
故④正确;
故选B.

【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数![]() 和
和![]() 的图象如图所示.
的图象如图所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣6 | ﹣4 | ﹣2 | 0 | ﹣2 | ﹣4 | ﹣6 | … |
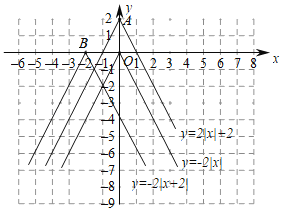
(1)观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解折式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点A,B的坐标和函数![]() 的对称轴.
的对称轴.
(2)探索思考:平移函数![]() 的图象可以得到函数
的图象可以得到函数![]() 和
和![]() 的图象,分别写出平移的方向和距离.
的图象,分别写出平移的方向和距离.
(3)拓展应用:在所给的平面直角坐标系内画出函数的图象.若点
![]() 和
和![]() 在该函数图象上,且
在该函数图象上,且![]() ,比较
,比较![]() ,
,![]() 的大小.
的大小.