题目内容
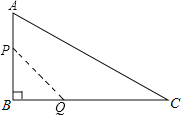
【题目】如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点D是AB的中点，点P是直线AC上一点，将△ADP沿DP所在的直线翻折后，点A落在A1处，若A1D⊥AC，则点P与点A之间的距离为______．
【答案】
或10
【解析】
分点
在AC左侧，点在AC右侧两种情况讨论，由勾股定理可
，由平行线分线段成比例可得
，可求AE，DE的长，由勾股定理可求AP的长．
解：分两种情况：
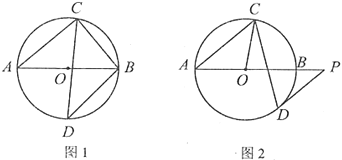
若点在AC左侧，如图1所示：
，
，
，
，
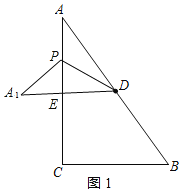
点D是AB的中点，
，
，
，
，
，
将
沿DP所在的直线翻折得
，
，
，
，
在
中，
，
，
；
若点在AC右侧，延长
交AC于E，如图2所示：
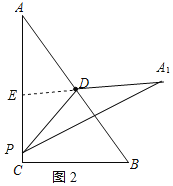
则
，
在
中，
，
，
，
故答案为：
或10．本题考查了翻折变换的性质、直角三角形的性质、勾股定理、分类讨论等知识，熟练掌握翻折变换的性质并进行分类讨论是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
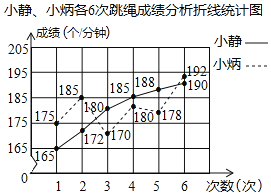
【题目】体育老师要从每班选取一名同学，参加学校的跳绳比赛．小静和小炳是跳绳能手，下面分别是小静、小炳各6次跳绳成绩统计图和成绩分析表
小静、小炳各6次跳绳成绩分析表
成绩 姓名 | 平均数 | 中位数 | 方差 |
小静 | 180 | 182.5 | 79.7 |
小炳 | 180 | a | 33 |
（1）根据统计图的数据，计算成绩分析表中a＝ ；
（2）结合以上信息，请你从两个不同角度评价这两位学生的跳绳水平．
