题目内容
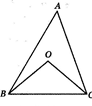
如图,点O是∠ABC的外心,∠A=50°,则∠BOC的度数是

| A.115° | B.130° | C.100° | D.120° |
C
分析:已知了点O是△ABC的外心,那么∠A、∠BOC即为同弧所对的圆周角和圆心角,根据圆周角定理即可得到∠BOC的度数.
解答:解:由于点O是△ABC的外心,所以在△ABC的外接圆⊙O中,
∠BAC、∠BOC同对着弧BC;
由圆周角定理得:∠BOC=2∠BAC=100°,
故选C.
解答:解:由于点O是△ABC的外心,所以在△ABC的外接圆⊙O中,
∠BAC、∠BOC同对着弧BC;
由圆周角定理得:∠BOC=2∠BAC=100°,
故选C.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
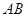 切
切 于点
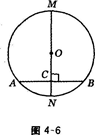
于点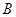 ,
,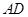 过圆心,且与
过圆心,且与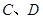 两点,连结
两点,连结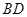 ,若
,若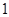 ,
,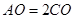 ,则
,则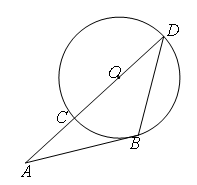
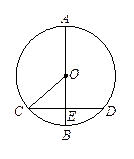
 ( )
( )
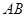 为
为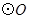 的直径,
的直径,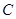 为
为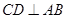 于
于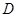 .
.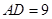 、
、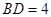 ,以
,以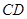 为半径的圆与
为半径的圆与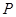 、
、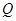 两点,弦
两点,弦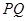 交
交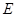 .则
.则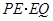 的值是( )
的值是( )