题目内容
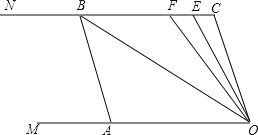
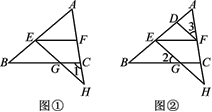
【题目】如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
【答案】(1)见解析;(2) 见解析.
【解析】
(1)由条件可证明∠AFE=∠BCF,根据平行线的判定可证明BC∥EF;
(2)由条件可先证明DF∥EH,可得∠DFE=∠FEG,再结合(1)的结论和已知条件可证明∠3=∠DFE,可证得结论.
证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.

练习册系列答案
相关题目