Question

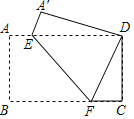
【题目】如图，AB为⊙O直径，PA、PC分别与⊙O相切于点A、C，PE⊥PA，PE交OC的延长线于点E．

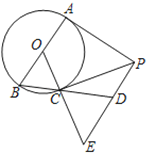
（1）求证：OE＝PE；

（2）连接BC并延长交PE于点D，PA＝AB，且CE＝9，求PE的长．

Answer 1

【答案】（1）证明见解析；（2）PE＝15．

【解析】

（1）连接OP，根据切线长定理可得PA=PC，OA⊥PA，利用SSS可证明△OPA≌△OPC，可得∠AOP＝∠POC，由PE⊥PA可得EP//BA，根据平行线的性质可得∠EPO＝∠AOP，即可证明∠EOP＝∠EPO，即可得OE=PE；（2）设OA＝r，由AB=PA可得PC=2r，由（1）得OE=PE，可得PE=r+9，根据切线的性质可得∠OCP＝∠PCE＝90°，利用勾股定理可求出r的值，进而可得PE的长.

（1）连接OP，

∵PA、PC分别与⊙O相切于点A，C

∴PA＝PC，OA⊥PA，

∵OA＝OC，OP＝OP，

∴△OPA≌△OPC（SSS），

∴∠AOP＝∠POC，

∵EP⊥PA，

∴EP∥BA，

∴∠EPO＝∠AOP，

∴∠EOP＝∠EPO，

∴OE＝PE．

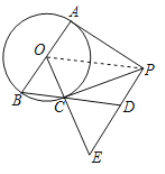
（2）设OC＝r．

∵AB=PA，PA=PC，AB=2OC，

∴PC=2OC=2r，

∵由（1）得OE＝PE，

∴PE=OC+CE=r+9,

∵PC是⊙O的切线，

∴OC⊥PC，

∴∠OCP＝∠PCE＝90°，

在Rt△PCE中，

∵PE2＝PC2+EC2，

∴（9+r）2＝92+（2r）2，

解得：r＝6或0（舍弃），

∴PE＝6+9=15．