题目内容
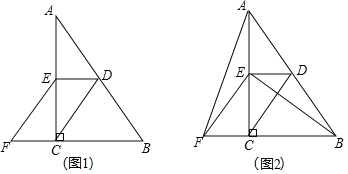
【题目】如图
，直线
与双曲线
相交于点
、
，与x轴相交于C点．
求点A、B的坐标及直线的解析式；
求
的面积；
观察第一象限的图象，直接写出不等式
的解集；
如图
，在x轴上是否存在点P，使得
的和最小？若存在，请说明理由并求出P点坐标．
【答案】（1）
（2）
（3）
（4）
【解析】
(1)先确定出点A，B坐标，再用待定系数法求出直线AB解析式；
(2)先求出点C，D坐标，再用面积的差即可得出结论；
(3)先确定出点P的位置，利用三角形的三边关系，最后用待定系数法求出解析式，即可得出结论．
点
、
在双曲线
上，
，
，
，
，
点A，B在直线
上，
，
，
直线AB的解析式为；
如图
，
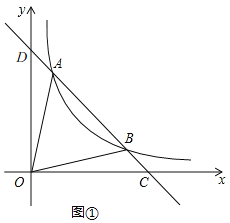
由
知，直线AB的解析式为，
，
，
，
，
；
由知，
，，
由图象知，不等式
的解集为；
存在，理由：如图2，
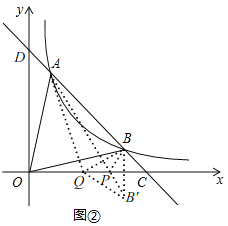
作点关于x轴的对称点B′（4，-1），连接AB′交x轴于点P，连接BP，在x轴上取一点Q，连接AQ，BQ，
点B与点B′关于x轴对称，
点P，Q是BB′的中垂线上的点，
∴PB′=PB， QB′=QB，
在△AQB′中，AQ+B′Q>AB′
的最小值为AB′，
，B ′（4，-1），
直线AB′的解析式为
，
令
，
，
，
．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
【题目】某地新建的一个企业，每月将生产1960吨污水，为保护环境，该企业计划购置污水处理器，并在如下两个型号种选择：
污水处理器型号 | A型 | B型 |
处理污水能力（吨/月） | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元，售出的1台A型、4台B型污水处理器的总价为42万元．
（1）求每台A型、B型污水处理器的价格；
（2）为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器，那么他们至少要支付多少钱？
