题目内容
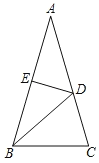
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为半径
为半径![]() 的中点,过
的中点,过![]() 作
作![]() 交弦
交弦![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() .
.
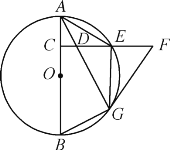
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 的半径为4.
的半径为4.
【解析】
(1)连接![]() ,由等边对等角的性质可得:
,由等边对等角的性质可得:![]() ,
,![]() ,由垂线的性质和三角形内角和定理可得:∠OAG+∠ADC=90°,等角代换可得; ∠OGA+∠DGF=90°,继而根据切线的判定即可求证结论;
,由垂线的性质和三角形内角和定理可得:∠OAG+∠ADC=90°,等角代换可得; ∠OGA+∠DGF=90°,继而根据切线的判定即可求证结论;
(2)连接![]() ,先求证
,先求证![]() 是等边三角形,由等边三角形的性质可得
是等边三角形,由等边三角形的性质可得![]() ,继而由同弧所对的圆周角等于其所对的圆心角的一半即可求解
,继而由同弧所对的圆周角等于其所对的圆心角的一半即可求解![]() 的度数;
的度数;
(3)过点![]() 作
作![]() 于点
于点![]() ,先征得
,先征得![]() ,在利用三角函数值求得:
,在利用三角函数值求得: ![]() ,
,![]() ,然后求证由相似三角形的判定方法
,然后求证由相似三角形的判定方法![]() ,由相似三角形的性质可得:
,由相似三角形的性质可得:![]() ,进而设
,进而设![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,代入,解方程即可求解.
,代入,解方程即可求解.
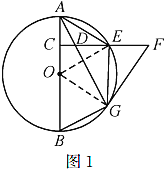
(1)证明:如图1,连接![]() .
.
∵![]() ,
,![]() ,
,
∵![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 是
是![]() 的切线.
的切线.
(2)解:如图1,连接![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() .
.
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() .
.
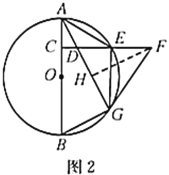
(3)如图2,过点![]() 作
作![]() 于点
于点![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
∴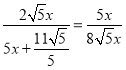 ,
,
解得:![]() ,
,
∴![]() ,
,
∴![]() 的半径为4.
的半径为4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:
营业员 | 嘉琪 | 嘉善 |
月销售件数/件 | 400 | 300 |
月总收入/元 | 7800 | 6600 |
假设月销售件数为x件,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员嘉善某月总收入不低于4200元,那么嘉善当月至少要卖多少件衣服?