Question

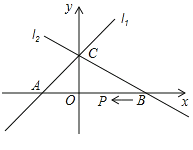
【题目】已知，如图直线的解析式为y=x+1，直线的解析式为；这两个图象交于y轴上一点C，直线与x轴的交点B（2，0）．

（1）求a、b的值；

（2）动点P从点B出发沿x轴以每秒1个单位长的速度向左移动，设移动时间为t秒，当△PAC为等腰三角形时，直接写出t的值．

Answer 1

【答案】（1）a，b=1；（2）t为1秒，2秒，或（）秒或（）秒．

【解析】

（1）先确定出点C的坐标，进而求出b，再将点B（2，0）代入直线l2的解析式中即可求出b；

（2）分三种情况讨论计算即可得出结论．

（1）∵点C是直线l1：y=x+1与轴的交点，∴C（0，1）．

∵点C在直线l2上，∴b=1，∴直线l2的解析式为y=ax+1．

∵点B在直线l2上，∴2a+1=0，∴a；

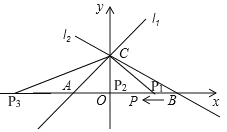
（2）如图，∵△PAC是等腰三角形，∴分三种情况讨论：

①当AC=P1C时．

∵CO⊥x轴，∴OP1=OA=1，∴BP1=OB﹣OP1=2﹣1=1，∴t=1÷1=1（秒）；

②当P2A=P2C时，易知点P2与O重合，∴BP2=OB=2，∴t=2÷1=2（秒）；

③当AP3=AC时．

∵A（﹣1，0），C（0，1），∴AC，∴AP3，∴BP3=OB+OA+AP3=3或BP3=OB+OA﹣AP3=3，∴t=（3）÷1=（3）（秒），或t=（3）÷1=（3）（秒）．

综上所述：满足条件的时间t为1秒，2秒，或（）或（）秒．