题目内容
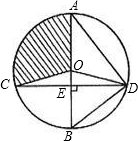
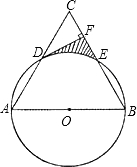
如图，已知⊙O的直径AB垂直于弦CD于E，连接AD、BD、OC、OD，且OD=5．
（1）若sin∠BAD=
，求CD的长；
（2）若∠ADO：∠EDO=4：1，求扇形OAC（阴影部分）的面积（结果保留π）．
（1）若sin∠BAD=
| 3 |
| 5 |
（2）若∠ADO：∠EDO=4：1，求扇形OAC（阴影部分）的面积（结果保留π）．
（1）∵AB是⊙O的直径，OD=5，
∴∠ADB=90°，AB=10，
在Rt△ABD中，sin∠BAD=
，sin∠BAD=
，
∴
=
，BD=6，
∴AD=
=
=8，
∵∠ADB=90°，AB⊥CD，
∴DE•AB=AD•BD，CE=DE，
∴DE×10=8×6，
∴DE=
∴CD=2DE=
；
（2）∵AB是⊙O的直径，AB⊥CD，
∴
=
，
=
，
∴∠BAD=∠CDB，∠AOC=∠AOD，
∵AO=DO，
∴∠BAD=∠ADO，
∴∠CDB=∠ADO，
设∠ADO=4x，则∠CDB=4x．
由∠ADO：∠EDO=4：1，则∠EDO=x．
∵∠ADO+∠EDB+∠EDO=90°，
∴4x+4x+x=90°，
解得：x=10°，
∴∠AOD=180°-（∠OAD+∠ADO）=100°，
∴∠AOC=∠AOD=100°，
∴S扇形OAC=
×π×52=
π．
∴∠ADB=90°，AB=10，
在Rt△ABD中，sin∠BAD=
| BD |
| AB |
| 3 |
| 5 |
∴
| BD |
| 10 |
| 3 |
| 5 |
∴AD=
| AB2-BD2 |
| 102-62 |
∵∠ADB=90°，AB⊥CD，
∴DE•AB=AD•BD，CE=DE，
∴DE×10=8×6，
∴DE=
| 24 |
| 5 |
∴CD=2DE=
| 48 |
| 5 |
（2）∵AB是⊙O的直径，AB⊥CD，
∴
 |
| CB |
|
| BD |
|
| AC |
|
| AD |
∴∠BAD=∠CDB，∠AOC=∠AOD，
∵AO=DO，
∴∠BAD=∠ADO，
∴∠CDB=∠ADO，
设∠ADO=4x，则∠CDB=4x．
由∠ADO：∠EDO=4：1，则∠EDO=x．
∵∠ADO+∠EDB+∠EDO=90°，
∴4x+4x+x=90°，
解得：x=10°，
∴∠AOD=180°-（∠OAD+∠ADO）=100°，
∴∠AOC=∠AOD=100°，
∴S扇形OAC=
| 100 |
| 360 |
| 125 |
| 18 |
练习册系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
由．
D、F．
BC，垂足为F
上的扇形都相同．