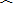题目内容
小芳同学在出黑板报时画出了一月牙形的图案如图，其中△AOB为等腰直角三角形，以O为圆心，OA为半径作扇形OAB，再以AB的中点C为圆心，以AB为直径作半圆，则月牙形阴影部分的面积S1与△AOB的面积S2之间的大小关系是（ ）
| A．S1＜S2 | B．S1=S2 | C．S1＞S2 | D．无法确定 |
设半径为r，则S△AOB=
r2
S扇形AOB=
=
S弓形=
利用勾股定理可知AB=
r
∴S扇形ABD=
=
∴S阴影=
-
=
．
故选B．
| 1 |
| 2 |
S扇形AOB=
| 90πr2 |
| 360 |
| πr2 |
| 4 |
S弓形=
| πr2-2r2 |
| 4 |
利用勾股定理可知AB=
| 2 |
∴S扇形ABD=
180π×(
| ||||
| 360 |
| πr2 |
| 4 |
∴S阴影=
| πr2 |
| 4 |
| πr2-2r2 |
| 4 |
| r2 |
| 2 |
故选B．
练习册系列答案
阅读快车系列答案
相关题目
