题目内容
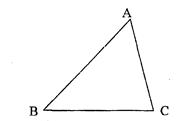
如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一
个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论:
①E为△ABP的外心; ②△PBE为等腰直角三角形;
③PC·OA = OE·PB; ④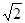 CE + PC的值不变.
CE + PC的值不变.
A.1个 B.2个 C.3个 D.4个
个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论:
①E为△ABP的外心; ②△PBE为等腰直角三角形;
③PC·OA = OE·PB; ④
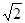 CE + PC的值不变.
CE + PC的值不变.A.1个 B.2个 C.3个 D.4个

C
解:①∵CO为等腰Rt△ABC斜边AB上的中线,
∴CO垂直平分AB;
又∵DE平分PB,即E点是AB、BP两边中垂线的交点,
∴E点是△ABP的外心,故①正确;
②如图,连接AE;

由①知:AE=EP=EB,则∠EAP=∠EPA,∠EPB=∠EBP,∠EAB=∠EBA;
∵∠PAB=45°,即∠EAP+∠EPA+∠EAB+∠EBA=2(∠EAP+∠EAB)=2∠PAB=90°,
由三角形内角和定理知:∠EPB+∠EBP=90°,即∠EPB=∠EBP=45°,
∴△PEB是等腰直角三角形;故②正确;
③∵∠PBE=∠ABC=45°,
∴∠EBO=∠PBC=45°-∠CBE,
又∵∠EOB=∠PCB=90°,
∴△BPC∽△BEO,得:PC/OE ="BC/OB" ,即PC•OB=OE•BC?PC•OA=OE•BC;
故③错误;
④过E作EM⊥OC,交AC于M;
 易知:△EMC是等腰直角三角形,即MC=
易知:△EMC是等腰直角三角形,即MC=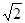 EC,∠PME=45°;
EC,∠PME=45°;
∴∠PEM=∠BEC=90°+∠PEC,
又∵EC=ME,PE=BE,
∴△PME≌△BCE(SAS),得PM=BC,即PM是定值;
由于PM=CM+PC=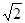 EC+PC,所以
EC+PC,所以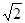 CE+PC的值不变,故④正确;
CE+PC的值不变,故④正确;
因此正确的结论是①②④,故选C.
∴CO垂直平分AB;
又∵DE平分PB,即E点是AB、BP两边中垂线的交点,
∴E点是△ABP的外心,故①正确;
②如图,连接AE;

由①知:AE=EP=EB,则∠EAP=∠EPA,∠EPB=∠EBP,∠EAB=∠EBA;
∵∠PAB=45°,即∠EAP+∠EPA+∠EAB+∠EBA=2(∠EAP+∠EAB)=2∠PAB=90°,
由三角形内角和定理知:∠EPB+∠EBP=90°,即∠EPB=∠EBP=45°,
∴△PEB是等腰直角三角形;故②正确;
③∵∠PBE=∠ABC=45°,
∴∠EBO=∠PBC=45°-∠CBE,
又∵∠EOB=∠PCB=90°,
∴△BPC∽△BEO,得:PC/OE ="BC/OB" ,即PC•OB=OE•BC?PC•OA=OE•BC;
故③错误;
④过E作EM⊥OC,交AC于M;
 易知:△EMC是等腰直角三角形,即MC=
易知:△EMC是等腰直角三角形,即MC=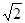 EC,∠PME=45°;
EC,∠PME=45°;∴∠PEM=∠BEC=90°+∠PEC,
又∵EC=ME,PE=BE,
∴△PME≌△BCE(SAS),得PM=BC,即PM是定值;
由于PM=CM+PC=
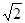 EC+PC,所以
EC+PC,所以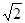 CE+PC的值不变,故④正确;
CE+PC的值不变,故④正确;因此正确的结论是①②④,故选C.

练习册系列答案
相关题目
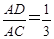 ,
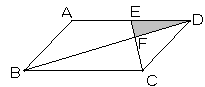
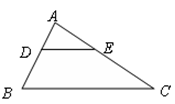
,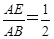 .试说明:△ADE∽△CDB
.试说明:△ADE∽△CDB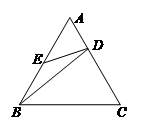
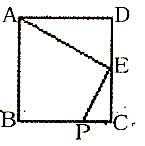
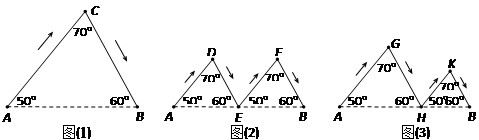

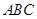 中,
中,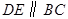 ,
, ,
,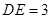 ,
,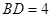 ,则
,则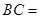 .
.
 中,点
中,点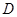 、
、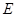 分别在边
分别在边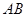 、
、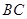 上,
上,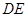 ∥
∥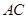 ,
, 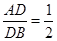 ,
,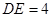 ,那么边
,那么边