��Ŀ����
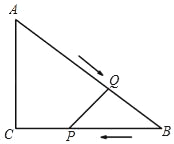
����Ŀ����֪����ͼ����Rt��ABC�У���C��90�㣬AC��3cm��BC��4cm����P�ӵ�B��������BC���C�����˶����ٶ�Ϊlcm/s��ͬʱ����Q�ӵ�A��������AB���B�����˶����ٶ�Ϊ2cm/s����һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶�����PQ�����˶�ʱ��Ϊt��s����0��t��2.5��������������⣺
��1����BQ���� ����BP���� �������ú�t�Ĵ���ʽ��ʾ��
�����PBQ�����Ϊy��cm2������ȷ��y��t�ĺ�����ϵʽ��
��2�����˶������У��Ƿ����ijһʱ��t��ʹ��PBQ�����Ϊ��ABC����Ķ���֮һ��������ڣ����t��ֵ�������ڣ���˵�����ɣ�
��3�����˶������У��Ƿ����ijһʱ��t��ʹ��BPQΪ���������Σ�������ڣ����t��ֵ�������ڣ���˵�����ɣ�
���𰸡���1����5��2t��t��y=��![]() t2+
t2+![]() t��2��������ijһʱ��t��ʹ��PBQ�����Ϊ��ABC����Ķ���֮һ��3��tΪ
t��2��������ijһʱ��t��ʹ��PBQ�����Ϊ��ABC����Ķ���֮һ��3��tΪ![]() ���
���![]() ���
���![]() ��ʱ����BPQΪ����������
��ʱ����BPQΪ����������
��������
��1���������ù��ɶ������AB�����ɵó����ۣ��ڹ���Q��QD��BC��D�������ó���BDQ�ס�BCA����t��ʾ��DQ������������ε������ʽ���ɵó����ۣ�
��2���������ABC���������������PBQ�����Ϊ��ABC����Ķ���֮һ����������t�ķ��̣������жϳ��˷����⣬���ɵó����ۣ�
��3����������������õ��������ε����ʺ����������ε����ʣ��ó�����ʽ��������t�ķ�����⣬���ɵó����ۣ�
��1������Rt��ABC��AC��3cm��BC��4cm��
���ݹ��ɶ����ã�AB��5cm��
���˶�֪��BP��t��AQ��2t��
��BQ��AB��AQ��5��2t��
�ʴ�Ϊ��5��2t��t��
����ͼ1������Q��QD��BC��D��

���BDQ����C��90����
�ߡ�B����B��
���BDQ�ס�BCA��
��![]() ��
��
��![]() ��
��
��DQ��![]() ��5��2t��
��5��2t��
��y��S��PBQ��![]() BPDQ��
BPDQ��![]() ��t��
��t��![]() ��5��2t������
��5��2t������![]() t2+
t2+![]() t��
t��
��2�������ڣ�
���ɣ���AC��3��BC��4��
��S��ABC��![]() ��3��4��6��
��3��4��6��
�ɣ�1��֪��S��PBQ����![]() t2+
t2+![]() t��
t��
�ߡ�PBQ�����Ϊ��ABC����Ķ���֮һ��
�ੁ![]() t2+
t2+![]() t��3��
t��3��
��2t2��5t+10��0��
�ߡ���25��4��2��10��0��
��˷����⣬
����������ijһʱ��t��ʹ��PBQ�����Ϊ��ABC����Ķ���֮һ��
��3���ɣ�1��֪��AQ��2t��BQ��5��2t��BP��t��
�ߡ�BPQ�ǵ��������Σ�
��ٵ�BP��BQʱ��
��t��5��2t��
��t��![]() ��
��
�ڵ�BP��PQʱ����ͼ2����P��PE��AB��E��

��BE��![]() BQ��
BQ��![]() ��5��2t����
��5��2t����
�ߡ�BEP��90������C����B����B��
���BEP�ס�BCA��
��![]() ��
��
��![]() ��
��
��t��![]()
�۵�BQ��PQʱ����ͼ3������Q��QF��BC��F��

��BF��![]() BP��
BP��![]() t��
t��
�ߡ�BFQ��90������C����B����B��
���BFQ�ס�BCA��
��![]() ��
��
��![]() ��
��
��t��![]() ��
��
����tΪ![]() ���
���![]() ���
���![]() ��ʱ����BPQΪ���������Σ�
��ʱ����BPQΪ���������Σ�