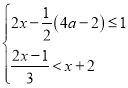题目内容
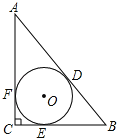
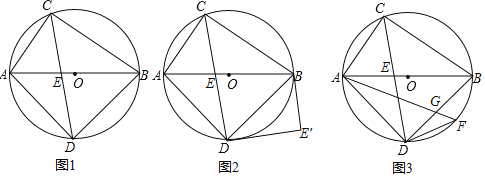
【题目】如图1,AB为⊙O的直径,点C为⊙O上一点,CD平分∠ACB交⊙O于点D,交AB于点E.
(1)求证:△ABD为等腰直角三角形;
(2)如图2,ED绕点D顺时针旋转90°,得到DE′,连接BE′,证明:BE′为⊙O的切线;
(3)如图3,点F为弧BD的中点,连接AF,交BD于点G,若DF=1,求AG的长.
【答案】(1)见解析;(2)见解析;(3)2.
【解析】
(1)由AB是⊙O的直径,根据直径所对的圆周角是直角,即可得∠ADB=90°,又由CD平分∠ACB,根据圆周角定理,可得AD=BD,继而可得△ABD是等腰直角三角形;
(2)证明△ADE≌△BDE',可得∠DAE=∠DBE',则∠OBE'=∠ABD+∠DBE'=90°,结论得证;
(3)取AG的中点H,连结DH,则DH=AH=GH,求出DH=DF=1,则答案可求出.
(1)∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵CD平分∠ACB,
∴∠ACD=∠DCB,
∴![]() ,
,
∴AD=BD,
∴△ABD是等腰直角三角形.
(2)由旋转的性质得,∠EDE'=90°,DE=DE',
∵∠ADB=90°,
∴∠ADE=∠BDE',
∵AD=BD,
∴△ADE≌△BDE'(SAS),
∴∠DAE=∠DBE',
∵∠EAD=∠DCB=45°,∠ABD=∠DCA=45°,
∴∠OBE'=∠ABD+∠DBE'=90°,
∴BE′为⊙O的切线;
(3)解:∵点F为![]() 的中点,
的中点,
∴∠FAD=![]() ∠DAB=22.5°,
∠DAB=22.5°,
取AG的中点H,连结DH,
∵∠ADB=90°,
∴DH=AH=GH,
∴∠ADH=∠FAD=22.5°,
∴∠DHF=∠ADH+∠FAD=45°,
∵∠AFD=∠ACD=45°,
∴∠DHF=∠AFD,
∴DH=DF=1,
∴AG=2DH=2.

练习册系列答案
相关题目