题目内容
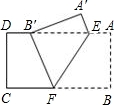
如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN.若CE的长为8cm,则MN的长为( )

| A.12cm | B.12.5cm | C.4
| D.13.5cm |

作NF⊥AD,垂足为F,连接AE,NE,
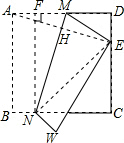
∵将正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,
∴∠D=∠AHM=90°,∠DAE=∠DAE,
∴△AHM∽△ADE,
∴∠AMN=∠AED,
又∵AD=NF,∠NFM=∠D=90°,
∴△NFM≌△ADE(AAS),
∴FM=DE=CD-CE=4cm,
又∵在Rt△MNF中,FN=12cm,
∴根据勾股定理得:MN=
=4
.
故选C.

∵将正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,
∴∠D=∠AHM=90°,∠DAE=∠DAE,
∴△AHM∽△ADE,
∴∠AMN=∠AED,
又∵AD=NF,∠NFM=∠D=90°,
∴△NFM≌△ADE(AAS),
∴FM=DE=CD-CE=4cm,
又∵在Rt△MNF中,FN=12cm,
∴根据勾股定理得:MN=
| FN2+FM2 |
| 10 |
故选C.

练习册系列答案
相关题目