题目内容
【题目】小华思考解决如下问题:
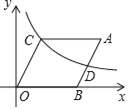
原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.
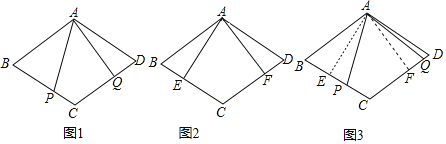
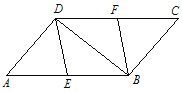
(1)小华进行探索,若将点P,Q的位置特殊化:把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E、F分别在边BC、CD上,如图2.此时她证明了AE=AF,请你证明;
(2)由以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F.请你继续完成原题的证明;
(3)如果在原题中添加条件:AB=4,∠B=60°,如图1,求四边形APCQ的周长的最小值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据四边形ABCD是菱形,首先证明∠B=∠D,AB=AD,再结合题意证明![]() ,进而证明△AEB≌△AFD,即可证明AE=AF.
,进而证明△AEB≌△AFD,即可证明AE=AF.
(2)根据(1)的证明,再证明△AEP≌△AFQ(ASA),进而证明AP=AQ.
(3)根据题意连接AC,则可证明△ABC为等边三角形,再计算AE的长度,则可计算长APCQ的周长的最小值.
(1)证明:如图2,∵四边形ABCD是菱形,
∴∠B+∠C=180°,∠B=∠D,AB=AD,
∵∠EAF=∠B,
∴∠EAF+∠C=180°,
∴∠AEC+∠AFC=180°,
∵AE⊥BC,
∴AF⊥CD,
在△AEB和△AFD中,
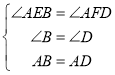 ,
,
∴△AEB≌△AFD(AAS),
∴AE=AF;
(2)证明:如图3,由(1)得,∠PAQ=∠EAF=∠B,AE=AF,
∴∠EAP=∠FAQ,
在△AEP和△AFQ中,
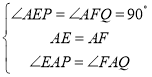 ,
,
∴△AEP≌△AFQ(ASA),
∴AP=AQ;
(3)解:如图4,连接AC,
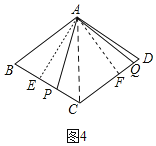
∵∠ABC=60°,BA=BC=4,
∴△ABC为等边三角形,
∵AE⊥BC,
∴BE=EC=2,
同理,CF=FD=2,
∴AE=![]() =2
=2![]() ,
,
∴四边形APCQ的周长=AP+PC+CQ+AQ=2AP+CP+CF+FQ=2AP+2CF,
∵CF是定值,当AP最小时,四边形APCQ的周长最小,
∴当AP=AE时,四边形APCQ的周长最小,此时四边形APCQ的周长的最小值=2×2![]() +4=4
+4=4![]() +4.
+4.