题目内容
已知a、b是关于x的一元二次方程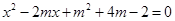
的两个实数根，那么
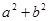的最小值是 ▲ ．
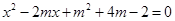的两个实数根，那么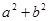的最小值是 ▲ ．
利用根与系数的关系可知：m+n=-2a，mn=a2+4a-2，则m2+n2=（m+n）2-2mn=4a2-2（a2+4a-2）=2a2-8a+4=2（a-2）2-4，此题还需考虑有实数根时a的取值范围，所以利用根的判别式求出a的取值范围，再利用二次函数的性质综合考虑求最小值则可．
解：∵△=（2m）2-4（m2+4m-2）≥0，
∴a≤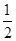
又∵a+b=-2m，ab=m2+4m-2，
∴a2+b2=（a+b）2-2ab=2（m-2）2-4，
根据二次函数的性质，m＜2时，函数值随a的增大而减小，
∴当m=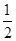时，m2+n2的值最小，
此时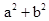
=2(-2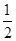)2-4=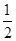，即最小值为．
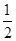解：∵△=（2m）2-4（m2+4m-2）≥0，
∴a≤
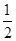
又∵a+b=-2m，ab=m2+4m-2，
∴a2+b2=（a+b）2-2ab=2（m-2）2-4，
根据二次函数的性质，m＜2时，函数值随a的增大而减小，
∴当m=
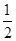时，m2+n2的值最小，此时
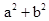=2(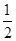-2)2-4=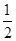，即最小值为．
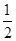练习册系列答案
阅读快车系列答案
相关题目
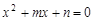的一个根，则
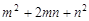的值为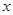 
（
，
、
、
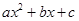
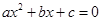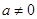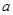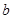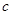为常数）一个解
的常数项为( )
的方程
是一元二次方程，则
＝ 
. 
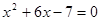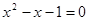
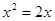的解为