��Ŀ����
����Ŀ��С����紴ҵ������һ��������Ϊ4Ԫ/ǧ�˵�ˮ��Ʒ�������г����鷢�֣�����ˮ��Ʒ����������y����ǧ�ˣ����ۼ�x��Ԫ/ǧ�ˣ�֮��Ĺ�ϵ��ͼ��ʾ��
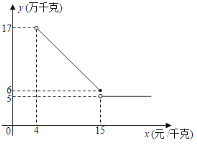
��1��������۴���ˮ��Ʒ����������y���ۼ�x֮��ĺ�������ʽ��
��2���г����黹���֣����۴���ˮ��Ʒ��Ҫ��Ͷ��ɱ�10��Ԫ�������������۹�������ˮ��Ʒ�����ʽ𣩣�����г��������Ź涨����ˮ��Ʒ�����ۼ۲�����20Ԫ/ǧ�ˣ������۴���ˮ��Ʒ�ۼ�Ϊ����Ԫʱ����õ��������������������Ƕ��٣�
���𰸡���1��y��![]() ����2�����۴���ˮ��Ʒ�ۼ�Ϊ20Ԫʱ����õ���������������������70��Ԫ
����2�����۴���ˮ��Ʒ�ۼ�Ϊ20Ԫʱ����õ���������������������70��Ԫ
��������
��1����4��x��15ʱ���躯������ʽΪy��kx+b������4��17������15��6�����뼴���������ʽ����x��15ʱ��y��5�����ɵõ��𰸣�
��2�����õ�������Ϊw��Ԫ���������������4��x��15ʱ���е�w����x��4������x+21����10������x��12.5��2+62.25�����ݺ��������ʵõ���x��12.5ʱ��w�����ֵΪ62.25��Ԫ����15��x��20ʱ���е�w����x��4����5��10��5x��30������һ�κ��������ʵõ���x��20ʱ��w�����ֵ��Ϊ70��Ԫ�����߱Ƚϼ��ɵõ�����
�⣺��1����4��x��15ʱ���躯������ʽΪy��kx+b������4��17������15��6������ã�
![]() ��
��
��ã�![]() ��
��
��y����x+21��
��x��15ʱ��y��5��
����������y���ۼ�x֮��ĺ�������ʽΪ��y��![]() .
.
��2�����õ�������Ϊw��Ԫ����������ã�
��4��x��15ʱ��
w����x��4������x+21����10
������x��12.5��2+62.25��
�߶�����ϵ��Ϊ��1��0��
�൱x��12.5ʱ��w�����ֵ��Ϊ62.25��Ԫ��
��15��x��20ʱ��
w����x��4����5��10��5x��30��
�൱x��20ʱ��w�����ֵ��Ϊ70��Ԫ��
��70��62.25��
�����۴���ˮ��Ʒ�ۼ�Ϊ20Ԫʱ����õ���������������������70��Ԫ��

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д� ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�