题目内容
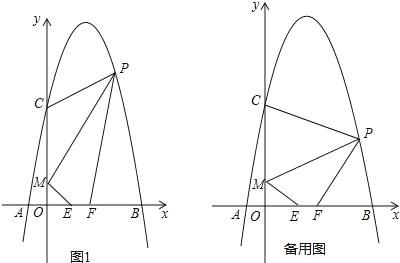
【题目】如图，对称轴为直线x=2的抛物线经过A（﹣1，0），C（0，5）两点，与x轴另一交点为B．已知M（0，1），E（a，0），F（a+1，0），点P是第一象限内的抛物线上的动点．
（1）求此抛物线的解析式；
（2）当a=1时，求四边形MEFP的面积的最大值，并求此时点P的坐标；
（3）若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？请说明理由．
【答案】（1）y=﹣（x﹣2）2+9=﹣x2+4x+5；
（2）当x=
时，四边形MEFP的面积有最大值为
，点P坐标为（，
）；
（3）a=
时，四边形PMEF周长最小，理由见解析．
【解析】
试题分析：（1）利用待定系数法求出抛物线的解析式；
（2）首先求出四边形MEFP面积的表达式，然后利用二次函数的性质求出最值及点P坐标；
（3）四边形PMEF的四条边中，PM、EF长度固定，因此只要ME+PF最小，则PMEF的周长将取得最小值．如答图3所示，将点M向右平移1个单位长度（EF的长度），得M1（1，1）；作点M1关于x轴的对称点M2，则M2（1，﹣1）；连接PM2，与x轴交于F点，此时ME+PF=PM2最小．
试题解析：方法一：
试题解析：（1）∵对称轴为直线x=2，
∴设抛物线解析式为y=a（x﹣2）2+k．
将A（﹣1，0），C（0，5）代入得：
，解得
，
∴y=﹣（x﹣2）2+9=﹣x2+4x+5．
（2）当a=1时，E（1，0），F（2，0），OE=1，OF=2．
设P（x，﹣x2+4x+5），
如答图2，过点P作PN⊥y轴于点N，则PN=x，ON=﹣x2+4x+5，
∴MN=ON﹣OM=﹣x2+4x+4．
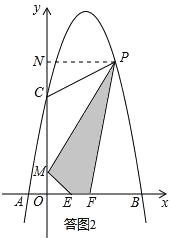
S四边形MEFP=S梯形OFPN﹣S△PMN﹣S△OME
=
（PN+OF）ON﹣PNMN﹣OMOE
=（x+2）（﹣x2+4x+5）﹣x（﹣x2+4x+4）﹣×1×1
=﹣x2+
x+
=﹣（x﹣
）2+
∴当x=
时，四边形MEFP的面积有最大值为，
把x=时，y=﹣（﹣2）2+9=
．
此时点P坐标为（，）．
（3）∵M（0，1），C（0，5），△PCM是以点P为顶点的等腰三角形，
∴点P的纵坐标为3．
令y=﹣x2+4x+5=3，解得x=2±
．
∵点P在第一象限，∴P（2+，3）．
四边形PMEF的四条边中，PM、EF长度固定，因此只要ME+PF最小，则PMEF的周长将取得最小值．
如答图3，将点M向右平移1个单位长度（EF的长度），得M1（1，1）；
作点M1关于x轴的对称点M2，则M2（1，﹣1）；
连接PM2，与x轴交于F点，此时ME+PF=PM2最小．
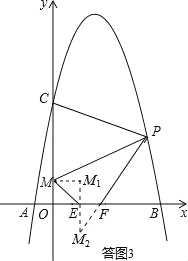
设直线PM2的解析式为y=mx+n，将P（2+，3），M2（1，﹣1）代入得：
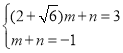，解得：m=
，n=﹣
，
∴y=x﹣．
当y=0时，解得x=
．∴F（，0）．
∵a+1=，∴a=
．
∴a=时，四边形PMEF周长最小．
方法二：
（1）略．
（2）连接MF，过点P作x轴垂线，交MF于点H，
显然当S△PMF有最大值时，四边形MEFP面积最大．
当a=1时，E（1，0），F（2，0），
∵M（0，1），
∴lMF：y=﹣
x+1，
设P（t，﹣t2+4t+5），H（t，﹣ t+1），
∴S△PMF=（PY﹣HY）（FX﹣MX），
∴S△PMF=（﹣t2+4t+5+t﹣1）（2﹣0）=﹣t2+
t+4，
∴当t=
时，S△PMF最大值为
，
∵S△MEF=EF×MY=×1×1=，
∴S四边形MEFP的最大值为+=
．
（3）∵M（0，1），C（0，5），△PCM是以点P为顶点的等腰三角形，
∴点P的纵坐标为3，∴﹣x2+4x+5=0，解得：x=2±
，
∵点P在第一象限，∴P（2+，3），PM、EF长度固定，
当ME+PF最小时，PMEF的周长取得最小值，
将点M向右平移1个单位长度（EF的长度），得M1（1，1），
∵四边形MEFM1为平行四边形，
∴ME=M1F，
作点M1关于x轴的对称点M2，则M2（1，﹣1），
∴M2F=M1F=ME，
当且仅当P，F，M2三点共线时，此时ME+PF=PM2最小，
∵P（2+，3），M2（1，﹣1），F（a+1，0），
∴KPF=KM1F，∴
，∴a=
．
