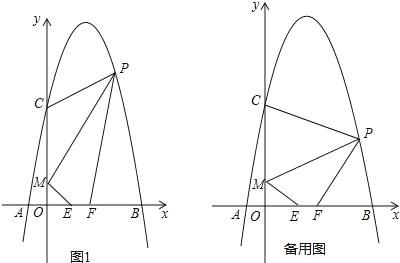
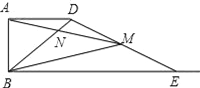
题目内容
【题目】如图,正方形ABCD的边长为10 cm,点E,F,G,H分别从点A,B,C,D出发,以2 cm/s的速度同时分别向点B,C,D,A运动.
(1)在运动的过程中,四边形EFGH是何种四边形?请说明理由.
(2)运动多少秒后,四边形EFGH的面积为52cm2?
【答案】(1)见解析;(2)运动2s或3s后,四边形EFGH的面积为52cm2.
【解析】试题分析:
试题解析:解:(1)四边形EFGH为正方形.理由如下:
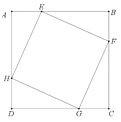
设运动时间为t s,则AE=BF=CG=DH=2tcm,
在正方形ABCD中,∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA,∴BE=CF=DG=AH.
在△AEH和△BFE中, 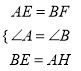 ,
,
∴△AEH≌△BFE,
同理可证:△AEH≌△BFE≌△CGF≌△DHG,∴EH=FE=GF=HG,
∴四边形EFGH为菱形.
∵△AEH≌△BFE,
∴∠AEH=∠BFE,而∠BFE+∠BEF=90°,
∴∠AEH+∠BEF=90°,
∴∠HEF=90°,
∴四边形EFGH为正方形.
(2)设运动的时间为x s,则AE=BF=CG=DH=2xcm.
∵AB=BC=CD=DA=10cm,
∴BE=CF=DG=AH=(10-2x)cm.
由勾股定理得S四边形EFGH=EH2=AE2+AH2=(2x)2+(10-2x)2=8x2-40x+100.
当S四边形EFGH=52 cm2时,8x2-40x+100=52,即x2-5x+6=0,
解得x1=2,x2=3.当x=2时,AE=2x=2×2=4<10;
当x=3时,AE=2x=2×3=6<10.
∴x=2或3均符合题意.故运动2s或3s后,四边形EFGH的面积为52cm2.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目