题目内容
【题目】如图,在四边形![]() 中,
中,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,且点
,且点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.

(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 的度数.
的度数.
【答案】(1)见解析;(2)∠AED=90°.
【解析】
(1)过点E作EF⊥AD于F,根据角平分线上的点到角的两边距离相等可得CE=EF,再求出BE=EF,然后根据到角的两边距离相等的点在角的平分线上证明;
(2)求出DC∥AB,求出∠CDA+∠BAD=180°,根据角平分线定义得出∠EAD=![]() ∠BAD,∠EDA=
∠BAD,∠EDA=![]() ∠CDA,求出∠EAD+∠EDA=90°,即可求出答案.
∠CDA,求出∠EAD+∠EDA=90°,即可求出答案.
(1)证明:如图,过点E作EF⊥AD于F,
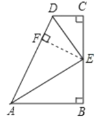
∵∠C=90°,DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴BE=EF,
又∵∠B=90°,EF⊥AD,
∴AE平分∠BAD;
(2)∵∠C=∠B=90°,
∴∠D+∠B=180°,
∴DC∥AB,
∴∠CDA+∠BAD=180°,
∵DE平分∠ADC,AE平分∠BAD,
∴∠EAD=![]() ∠BAD,∠EDA=
∠BAD,∠EDA=![]() ∠CDA,
∠CDA,
∴∠EAD+∠EDA=90°,
∴∠AED=180°90°=90°.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目





