��Ŀ����
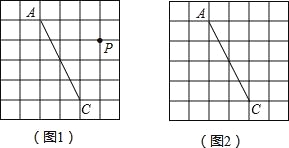
����Ŀ��ͼ1��ͼ2��������״�ʹ�С��ȫ��ͬ�ķ���ֽ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AC�������˵����С�����εĶ����ϣ�
��1����ͼ1����P��С�����εĶ����ϣ���ͼ1��������P����ֱ��AC�ĶԳƵ�Q������AQ��QC��CP��PA����ֱ��д���ı���AQCP���ܳ���
��2����ͼ2�л���һ�����߶�ACΪ�Խ��ߡ����Ϊ6�ľ���ABCD���ҵ�B�͵�D����С�����εĶ����ϣ�
���𰸡���1����ͼ��������![]() ����2����ͼ������.
����2����ͼ������.
��������
�����������1��ͨ�������ӿɵõ���P����AC�ĶԳƵ㣬��ֱ�����ù��ɶ����ɵõ��ܳ�����2�����������Ͼ��ε������Լ����ɶ����ɻ�������.
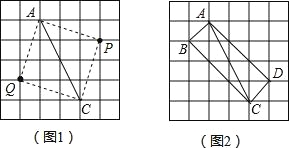
�����������1����ͼ1��ʾ���ı���AQCP��Ϊ���������ܳ�Ϊ��![]() ����2����ͼ2��ʾ���ı���ABCD��Ϊ����
����2����ͼ2��ʾ���ı���ABCD��Ϊ����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ�� (2016ɽ��Ϋ����20��)����5�£�ij������ҵ���������ȡ������m����ҵ������������������������갴�������ɼ��ֳ���A��B��C��D�ĸ��ȼ�����������ͼ�в�������ͳ��ͼ����
�����ɼ�n���֣� | �����ȼ� | Ƶ�� |
90��n��100 | A | 2 |
80��n��90 | B | |
70��n��80 | C | 15 |
n��70 | D | 6 |
����������Ϣ����������⣺
��1����m��ֵ��
��2��������ͳ��ͼ�У���B�ȼ��������ε�Բ�ĽǵĴ�С��������öȡ��֡����ʾ��
��3���������ɼ�������80�ֵ�����������ѡ2�ҽ���Ӫ�����飬������������һ����A�ȼ��ĸ��ʣ�
����Ŀ��ijУ�о���ѧϰС���ԡ�ѧ����ѧУ��ͨ�������͡�Ϊ�����ȫУѧ����������������飬�������Ŀ�У�����������С����Ħ�г������г���������ÿλͬѧ��ѡһ������ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
��ͨ��ʽ | Ƶ���������� | Ƶ�� |
�������� | m | 0.25 |
�� | 24 | 0.20 |
Ħ�г� | 36 | n |
���г� | 18 | 0.15 |
���� | 12 | 0.10 |
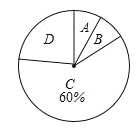
�����ͼ����Ϣ����������⣺
��1�����ι�����������ѧ����
��2����գ�Ƶ���ֲ����е�m= �� n=��
��3��������ͳ��ͼ�У���������Ħ�г������ڵ����ε�Բ�ĽǵĶ�����
