题目内容
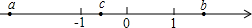 已知有理数a、b、c在数轴上的位置如图所示,则
已知有理数a、b、c在数轴上的位置如图所示,则| b+c | a |
<
<
0,|a+c|-2|c-b|化简的结果为-a-2b+c
-a-2b+c
.分析:根据有理数a、b、c在数轴上的位置,判断出a<0,c<0,b>0,|a|>|c|,|b|>|c|,再判断出b+c>0,a+c<0,c-b<0,然后把绝对值进行化简即可.
解答:解;∵有理数a、b、c在数轴上的位置如图,
∴a<0,c<0,b>0,|a|>|c|,|b|>|c|,
∴b+c>0,a+c<0,c-b<0,
∴
<0,|a+c|-2|c-b|=-a-c-2(b-c)=-a-c-2b+2c=-a-2b+c;
故答案为;<,-a-2b+c.
∴a<0,c<0,b>0,|a|>|c|,|b|>|c|,
∴b+c>0,a+c<0,c-b<0,
∴
| b+c |
| a |
故答案为;<,-a-2b+c.
点评:此题考查了整式的加减,用到的知识点是数轴、绝对值、整式的加减,关键是根据数轴判断出有理数的符号和绝对值.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目


 已知有理数a,b所对应的点在数轴上如图所示,化简|b-a|得( )
已知有理数a,b所对应的点在数轴上如图所示,化简|b-a|得( )