题目内容
【题目】如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( ) 
A.2.3
B.2.4
C.2.5
D.2.6
【答案】B
【解析】解:在△ABC中, ∵AB=5,BC=3,AC=4,
∴AC2+BC2=32+42=52=AB2 ,
∴∠C=90°,
如图:设切点为D,连接CD,
∵AB是⊙C的切线,
∴CD⊥AB,
∵S△ABC= ![]() ACBC=
ACBC= ![]() ABCD,
ABCD,
∴ACBC=ABCD,
即CD= ![]() =
= ![]() =
= ![]() ,
,
∴⊙C的半径为 ![]() ,
,
故选B.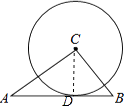
首先根据题意作图,由AB是⊙C的切线,即可得CD⊥AB,又由在直角△ABC中,∠C=90°,AC=3,BC=4,根据勾股定理求得AB的长,然后由S△ABC= ![]() ACBC=
ACBC= ![]() ABCD,即可求得以C为圆心与AB相切的圆的半径的长.
ABCD,即可求得以C为圆心与AB相切的圆的半径的长.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目