题目内容
【题目】如图,二次函数y=![]() x2+2x+6的图像与x轴相交于A、B两点,与y轴交于点C,顶点为点D,该二次函数图像的对称轴与直线BC相交于点E,与x轴交于点F;
x2+2x+6的图像与x轴相交于A、B两点,与y轴交于点C,顶点为点D,该二次函数图像的对称轴与直线BC相交于点E,与x轴交于点F;
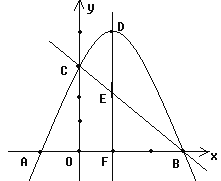
(1)求直线BC的解析式;
(2)试判断△BFE与△DCE是否相似?并说明理由.
(3)在坐标轴上是否存在这样的点P,使得以点P、B、C为顶点的三角形与△DCE相似?若存在,请求出点P的坐标;若不存在,请说明理由。
【答案】(1) y=-x+6.(2) △BFE与△DCE相似.理由见解析;(3)在坐标轴上存在这样的点P,使得以点P、B、C为顶点的三角形与△DCE相似,P点的坐标为(0,0)、(-6,0)和(0,-6).
【解析】
试题分析:(1)令x=0,可求得C点坐标,令y=0,可求得A、B点坐标,设出直线BC解析式,由待定系数法即可得出结论;
(2)观察两三角形可知,存在一个对顶角,只需再有一个角相等即可,由于DF⊥x轴,在△DCE中只要找到一个直角即可,结合边的长度由勾股定理可得出结论;
(3)结合(2)的结论,只要找到以点P、B、C为顶点的三角形与△BFE相似即可,分BC为斜边,直角边讨论即可.
试题解析:(1)令x=0,则有y=6,
∴C点坐标为(0,6);
令y=0,则有-![]() x2+2x+6=0,
x2+2x+6=0,
解得:x1=-2,x2=6,
∴A点坐标为(-2,0),B点坐标为(6,0).
设直线BC的解析式为y=kx+b,
则有![]() ,解得:
,解得:![]() .
.
∴直线BC的解析式为y=-x+6.
(2)假设△BFE与△DCE相似.
∵二次函数y=-![]() x2+2x+6=-
x2+2x+6=-![]() (x-2)2+8,
(x-2)2+8,
∴D点坐标为(2,8),直线DE解析式为x=2.
∵直线BC、DE相交于点E,
∴![]() ,解得
,解得![]() ,
,
即点E坐标为(2,4).
∵点C(0,6),点D(2,8),
∴DE=4,CE=![]() ,CD=
,CD=![]() ,
,
∴DE2=CE2+CD2,
∴∠DCE=90°.
又∵∠BFE=90°,且∠DEC=∠BEF,
∴△DCE∽△BEF.
(3)假设存在.
由(2)可知△DCE∽△BEF,
故只需找到以点P、B、C为顶点的三角形与△BEF相似即可.
①以BC为斜边,如图1.
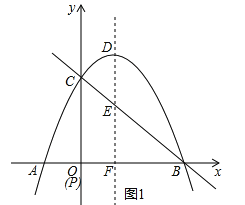
此时P点与O点重合,故P点坐标为(0,0);
②以BC为直角边,点P在x轴上,如图2.
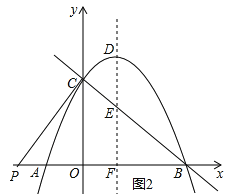
∵点C(0,6),点B(6,0),
∴BO=6,CO=6,
∴∠OBC=∠OCB=45°,BC=![]() ,
,
∴BP=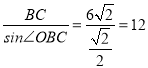 ,
,
∴P点坐标为(-6,0);
③以BC为直角边,点P在y轴上,如图3.
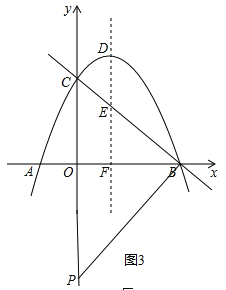
CP=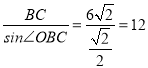 ,
,
∴P点坐标为(0,-6).
综上可知:在坐标轴上存在这样的点P,使得以点P、B、C为顶点的三角形与△DCE相似,P点的坐标为(0,0)、(-6,0)和(0,-6).

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案