题目内容
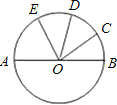如图，已知：AB是⊙O的直径，C、D是
上的三等分点，∠AOE=60°，则∠COE是
- A.40°
- B.60°
- C.80°
- D.120°
C
分析：先求出∠BOE=120°，再运用“等弧对等角”即可解．
解答：∵∠AOE=60°，
∴∠BOE=180°-∠AOE=120°，
∴的度数是120°，
∵C、D是上的三等分点，
∴弧CD与弧ED的度数都是40度，
∴∠COE=80°．
故选C．
点评：本题利用了邻补角的概念和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
分析：先求出∠BOE=120°，再运用“等弧对等角”即可解．
解答：∵∠AOE=60°，
∴∠BOE=180°-∠AOE=120°，
∴
的度数是120°，∵C、D是
上的三等分点，∴弧CD与弧ED的度数都是40度，
∴∠COE=80°．
故选C．
点评：本题利用了邻补角的概念和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
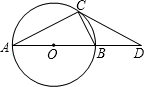如图，已知：AB是⊙O的直径，BD=OB，∠CAB=30°，请根据已知条件和所给图形，写出8个正确的结论（除AO=OB=BD外）．
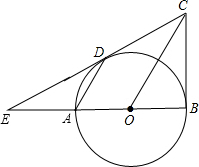CD的延长线的交点．
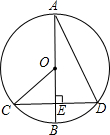如图，已知：AB是⊙O的直径，CD⊥AB于E，连接AD、OC．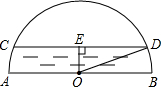
如图，已知：AB是⊙O的弦，C是AB上的点，AC=4、BC=1、OC=2，则⊙O的半径是