题目内容
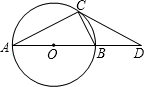 如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).
如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).
分析:首先发现30°的直角三角形ABC,若连接OC,则进一步发现等边三角形OBC和30°的直角三角形OCD,然后根据等边三角形的性质、30度的直角三角形的性质以及切线的判定定理和性质得到有关结论.
解答: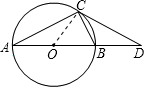 解:连接OC,
解:连接OC,
∵AB是⊙O的直径,BD=OB,∠CAB=30°,
∴∠ACB=90°,OA=OB=OC,∠ABC=60°,
∴∠D=30°,DC是⊙O的切线;
△CBD是等腰三角形,△ACD是等腰三角形,
AC=CD,BD=BC,△DCB∽△DAC,
DC2=DB•DA,AC=
BC,AD=
CD等.
 解:连接OC,
解:连接OC,∵AB是⊙O的直径,BD=OB,∠CAB=30°,
∴∠ACB=90°,OA=OB=OC,∠ABC=60°,
∴∠D=30°,DC是⊙O的切线;
△CBD是等腰三角形,△ACD是等腰三角形,
AC=CD,BD=BC,△DCB∽△DAC,
DC2=DB•DA,AC=
| 3 |
| 3 |
点评:此题要能够熟练运用圆周角定理及其推论、30°的直角三角形的性质和等边三角形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
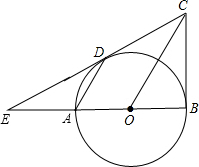 CD的延长线的交点.
CD的延长线的交点.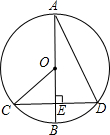 如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.
如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.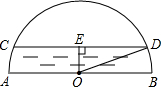

 如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是