题目内容
 如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
| ||
| 2 |
| ||
| 2 |
分析:过O作OD⊥AB于D,连接OA,求出AD、BD,根据勾股定理求出OD,根据勾股定理求出OA.
解答:解: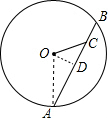
过O作OD⊥AB于D,连接OA,
AB=AC+BC=4+1=5,
∵OD⊥AB,OD过O,
∴AD=BD=
AB=
,
∴DC=
,
在Rt△COD中,由勾股定理得:OD=
=
,
在Rt△AOD中,由勾股定理得:OA=
=
,
故答案为:
.

过O作OD⊥AB于D,连接OA,
AB=AC+BC=4+1=5,
∵OD⊥AB,OD过O,
∴AD=BD=
| 1 |
| 2 |
| 5 |
| 2 |
∴DC=
| 3 |
| 2 |
在Rt△COD中,由勾股定理得:OD=
22-(
|
| ||
| 2 |
在Rt△AOD中,由勾股定理得:OA=
(
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了勾股定理,垂径定理的应用,关键是构造直角三角形后求出各个线段的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
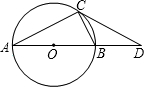 如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).
如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).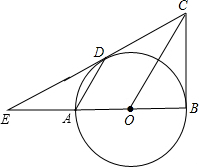 CD的延长线的交点.
CD的延长线的交点.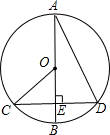 如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.
如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.
