题目内容
如图,已知:AB是⊙O的直径,BC、CD分别是⊙O的切线,切点分别为B、D,E是BA和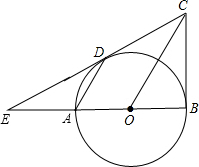 CD的延长线的交点.
CD的延长线的交点.(1)猜想AD与OC的位置关系,并加以证明;
(2)设AD•OC的积为S,⊙O的半径为r,试探究S与r的关系;
(3)当r=2,sin∠E=
| 1 | 3 |
分析:(1)连接OD,由切线长定理可证得∠COD=∠COB,由圆周角定理得到∠DAB=
∠BOD=
(∠COB+∠COD)=∠COB,再由同位角相等,两直线平行得AD∥OC;
(2)连接BD,可证得Rt△ABD∽Rt△OCB?
=
,S=AD•OC=AB•OB=2r•r=2r2,即S=2r2;
(3)在Rt△OED中,
=sin∠E=
?OE=3OD,OA=OD?AE=2OA,由AD∥OC?
=
?AD=
OC又∵AD•OC=2r2=8,由此得到关于AD,OC的方程组,解之即可求出OC,AD的值.
| 1 |
| 2 |
| 1 |
| 2 |
(2)连接BD,可证得Rt△ABD∽Rt△OCB?
| AD |
| OB |
| AB |
| OC |
(3)在Rt△OED中,
| OD |
| OE |
| 1 |
| 3 |
| AD |
| OC |
| AE |
| OE |
| 2 |
| 3 |
解答: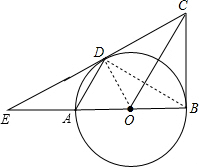 解:(1)猜想:AD∥OC,
解:(1)猜想:AD∥OC,
证明:连接OD,
∵CB、CD分别切⊙O于B、D两点,
∴CB=CD,∠CDO=∠CBO=90°,
∠OCB=∠OCD,
∴∠COD=∠COB;
又∵∠DAB=
∠BOD=
(∠COB+∠COD)
∴∠DAB=∠COB,
∴AD∥OC.
(2)连接BD.
在△ABD和△OCB中,
∵AB是直径,
∴∠ADB=∠OBC=90°,
又∵∠COB=∠BAD
∴Rt△ABD∽Rt△OCB,
∴
=
,
S=AD•OC=AB•OB=2r•r=2r2,
即S=2r2;
(3)在Rt△OED中,
∵∠ODE=90°,sin∠E=
,
∴
=sin∠E=
,
∴OE=3OD.
∵OA=OD,
∴AE=2OA;
∵AD∥OC,
∴
=
,
∴AD=
OC,
又∵AD•OC=2r2=8,AD>0,OC>0,
∴
,
解之,得OC=2
,AD=
.
即AD,OC的值分别为
,2
.
 解:(1)猜想:AD∥OC,
解:(1)猜想:AD∥OC,证明:连接OD,
∵CB、CD分别切⊙O于B、D两点,
∴CB=CD,∠CDO=∠CBO=90°,
∠OCB=∠OCD,
∴∠COD=∠COB;
又∵∠DAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DAB=∠COB,
∴AD∥OC.
(2)连接BD.
在△ABD和△OCB中,
∵AB是直径,
∴∠ADB=∠OBC=90°,
又∵∠COB=∠BAD
∴Rt△ABD∽Rt△OCB,
∴
| AD |
| OB |
| AB |
| OC |
S=AD•OC=AB•OB=2r•r=2r2,
即S=2r2;
(3)在Rt△OED中,
∵∠ODE=90°,sin∠E=
| 1 |
| 3 |
∴
| OD |
| OE |
| 1 |
| 3 |
∴OE=3OD.
∵OA=OD,
∴AE=2OA;
∵AD∥OC,
∴
| AD |
| OC |
| AE |
| OE |
∴AD=
| 2 |
| 3 |
又∵AD•OC=2r2=8,AD>0,OC>0,
∴
|
解之,得OC=2
| 3 |
| 4 |
| 3 |
| 3 |
即AD,OC的值分别为
| 4 |
| 3 |
| 3 |
| 3 |
点评:本题利用了切线长定理,切线的性质,直角三角形的性质,等边对等角相似三角形的判定和性质,正弦的概念,平行线的判定和性质等知识求解,综合性比较强.

练习册系列答案
相关题目
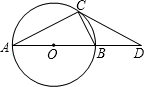 如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).
如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).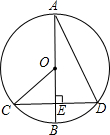 如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.
如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.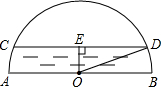

 如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是