题目内容
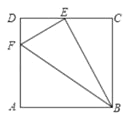
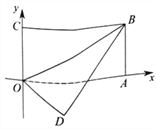
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,把矩形
,把矩形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,则点
处,则点![]() 的坐标为__________.
的坐标为__________.
【答案】![]()
【解析】由折叠的性质得到一对角相等,再由矩形对边平行得到一对内错角相等,等量代换及等角对等边得到BE=OE,利用AAS得到三角形OED与三角形BEA全等,由全等三角形对应边相等得到DE=AE,过D作DF垂直于OE,利用勾股定理及面积法求出DF与OF的长,即可确定出D坐标.
由折叠得:∠CBO=∠DBO,
∵矩形ABCO,
∴BC∥OA,
∴∠CBO=∠BOA,
∴∠DBO=∠BOA,
∴BE=OE,
在△ODE和△BAE中,
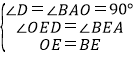 ,
,
∴△ODE≌△BAE(AAS),
∴AE=DE,
设DE=AE=x,则有OE=BE=8-x,
在Rt△ODE中,根据勾股定理得:42+(8-x)2=x2,
解得:x=5,即OE=5,DE=3,
过D作DF⊥OA,
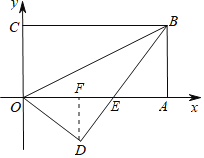
∵S△OED=![]() ODDE=
ODDE=![]() OEDF,
OEDF,
∴DF=![]() ,OF=
,OF=![]() ,
,
则D(![]() ,-
,-![]() ).
).
故答案为:(![]() ,-
,-![]() ).
).

 每日10分钟口算心算速算天天练系列答案
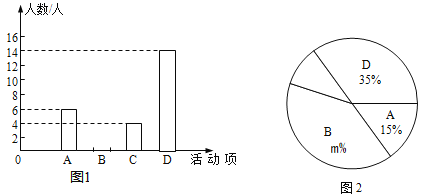
每日10分钟口算心算速算天天练系列答案【题目】七(1)班同学为了解2017年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量 | 频数(户数) | 百分比 |
| 6 |
|
|
| |
| 16 |
|
| 10 |
|
| 4 | |
| 2 |
|

(1)请将下列频数分布表和频数分布直方图补充完整;
(2)求该小区月均用水量不超过![]() 的家庭占被调查家庭总数的百分比;
的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过![]() 的家庭数.
的家庭数.
【题目】下表是某校七﹣九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,但表格中九年级的两个数据被遮盖了,记得九年级文艺小组活动次数与科技小组活动次数相同.
年级 | 课外小组活动总时间(单位:h) | 文艺小组活动次数 | 科技小组活动次数 |
七年级 | 17 | 6 | 8 |
八年级 | 14.5 | 5 | 7 |
九年级 | 12.5 |
|
|
则九年级科技小组活动的次数是_____.